座標平面上で円はどのような方程式で表されるのでしょうか。
・円の方程式
円は、ある点(中心)からの距離が同じである点の集合です。
中心の点の座標を\(C(a,b)\)とすると、半径\(r(>0)\)の円は \(CP=r=\)(一定) を満たす点\(P\)全体の集合となります。
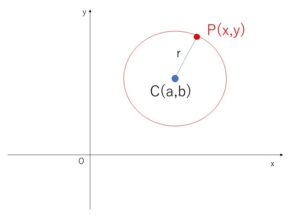
\(P(x,y)\)とすると、\(CP=r\) より
\(\sqrt{(x-a)^2+(y-b)^2}=r\)
つまり
\((x-a)^2+(y-b)^2=r^2\)
これが中心\((a,b)\),半径\(r\)の円の方程式となります。
とくに中心が原点のとき \(a=b=0\) なので
\(x^2+y^2=r^2\) です。
\((x-a)^2+(y-b)^2=r^2\)
とくに中心が原点のとき
\(x^2+y^2=r^2\)
また、円の方程式 \((x-a)^2+(y-b)^2=r^2\) を展開すると
\(x^2-2ax+y^2-2by+a^2+b^2-r^2=0\)
となり、係数部分を別の文字で置き換えると、この式は次のような形となります。
\(x^2+y^2+lx+my+n=0\)・・・① (円の方程式の一般形)
方程式①の特徴は、
・\(x^2,y^2\)の係数が等しい
・\(xy\)の項が無い\(x,y\)の2次式
となっています。
なお、円であれば①の形に表されることが分かりましたが、逆に①の形の方程式は(必ず)円を表すかどうかについては →(3-3)2次の方程式の表す図形 で扱っていきます。
(例題)次の円の方程式を求めよ。
(1)点\((3,-2)\)を中心とし、点\((1,4)\)を通る円
(2)2点 \((1,4)\),\((5,6)\)を直径の両端とする円
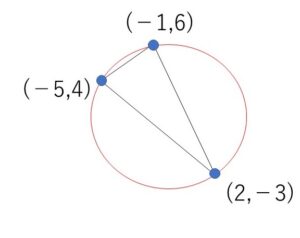
(3)3点 \((-5,4)\),\((-1,6)\),\((2,-3)\) を通る円
(解答)
(1)
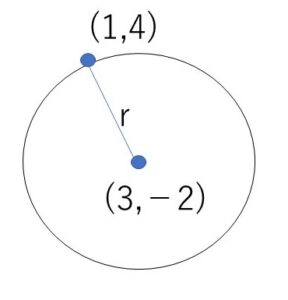
中心\((3,-2)\) と \((1,4)\)の距離は
\(\sqrt{(-2)^2+6^2}\)\(=\sqrt{40}\)
これが半径なので円の方程式は
\((x-3)^2+(y+2)^2=40\)
(2)
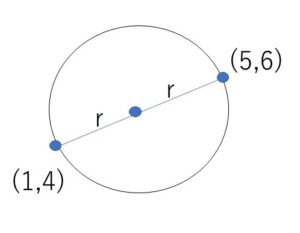
円の中心は 2点 \((1,4)\),\((5,6)\) の中点なので、その座標は
\((3,5)\)
また、半径は \((3,5)\)と\((1,4)\)の距離より
\(\sqrt{(-2)^2+(-1)^2}\)\(=\sqrt{5}\)
よって円の方程式は
\((x-3)^2+(y-5)^2=5\)
(3)
円の方程式を \(x^2+y^2+lx+my+n=0\)・・・(A) とする。
3点 \((-5,4)\),\((-1,6)\),\((2,-3)\)を通るので、(A)に代入して
\(25+16-5l+4m+n=0\)・・・(ア)
\(1+36-l+6m+n=0\)・・・(イ)
\(4+9+2l-3m+n=0\)・・・(ウ)
(イ)-(ア), (ウ)-(イ)より
\(4l+2m-4=0\)・・・(エ)
\(3l-9m-24=0\)・・・(オ)
(エ)(オ)より \(l,m\)を求めると
\(l=2\), \(m=-2\)
(ウ)より \(n=-23\)
したがって円の方程式は
\(x^2+y^2+2x-2y-23=0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の方程式② back→座標を利用した証明(直線の方程式)