円の方程式②

円の方程式に関する色々な問題について見ていきます。

(例題1)
(1)直線 \(y=-4x+5\) 上に中心をもち、\(x\)軸と\(y\)軸の両方に接する円の方程式を求めよ。
(2)点\((8,6)\)を通り、\(y\)軸と接する円のうちで、半径が最も小さい円の方程式を求めよ。

(解答)
(1)

円の中心の座標を \((k,-4k+5)\)とおくと、円が\(x\)軸と\(y\)軸に接するので、半径を\(r\)として
\(|k|=|-4k+5|=r\)

\(|k|=|-4k+5|\)　より
\(k=±(-4k+5)\)
よって、 \(k=1,\displaystyle\frac{5}{3}\)

\(k=1\)のとき \(r=1\)で 中心の座標は\((1,1)\)なので円の方程式は
\((x-1)^2+(x-1)^2=1\)

\(k=\displaystyle\frac{5}{3}\) のとき \(r=\displaystyle\frac{5}{3}\) で、中心の座標は \((\displaystyle\frac{5}{3},-\displaystyle\frac{5}{3})\) なので円の方程式は
\((x-\displaystyle\frac{5}{3})^2+(y+\displaystyle\frac{5}{3})^2=\displaystyle\frac{25}{9}\)

答え \((x-1)^2+(x-1)^2=1\),　\((x-\displaystyle\frac{5}{3})^2+(y+\displaystyle\frac{5}{3})^2=\displaystyle\frac{25}{9}\)

(2)

条件を満たす円は\(y\)軸から右側にあります。
また、中心を\(C\),\(y\)軸との接点を\(T\)とおくと、円の半径が最も小さくなるときは、直線\(CT\)上に\((8,6)\)があるとき(\(T\)と\((8,6)\)を結ぶ線分が直径となるとき)です。なぜなら、\(CT\)上に\((8,6)\)がない場合は、直径が\(8\)より大きくなるからです。

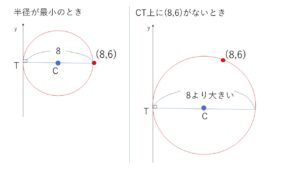
求める円の中心の\(x\)座標は正の値。
また、円の半径が最も小さくなるのは、円と\(y\)軸の接点\(T\)と円の中心\(C\)を結ぶ直線上に\((8,6)\)があるときである。このとき\(T\)と\((8,6)\)を結ぶ線分は円の直径となる。
よって半径は \(4\)。
\(T(0,6)\)より円の中心の座標は\(T\)と\((8,6)\)の中点だから、\((4,6)\)

したがって円の方程式は
\((x-4)^2+(y-6)^2=16\)

(別解)中心を\((a,b)\)とおいて、半径が最小となる\(a,b\)を決定する方法
円の中心の座標を \((a,b)\)とおく。(\(a>0\))

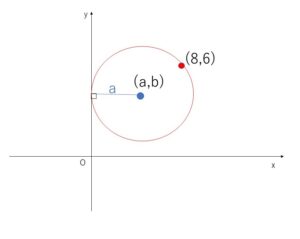
円は\(y\)軸に接するので半径は\(a\)だから、円の方程式は
\((x-a)^2+(y-b)^2=a^2\)・・・①

\((8,6)\)を通るので①に代入して
\((8-a)^2+(6-b)^2=a^2\)
\((6-b)^2\)以外を展開して整理すると
\(a=\displaystyle\frac{1}{16}(6-b)^2+4\)

半径\(a\)が最小となるとき \(b=6\)で、このとき\(a=4\)
①より
\((x-4)^2+(y-6)^2=16\)

(例題2)
\(x\)軸上の正の部分を動く点\(P(t,0)\) (\(t>0\))と2点 \(A(0,1)\),\(B(0,3)\)がある。
(1)3点 \(A,B,P\) を通る円の中心の座標を求めよ。
(2)2点 \(A,B\) を通り、\(x\)軸の正の部分に接する円の方程式を求めよ。
(3)\(\angle APB\) を最大にする点\(P\)の座標を求めよ。

(解答)
(1)

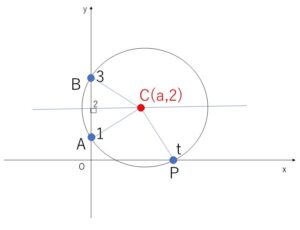
中心\(C\)は、\(A,B\)の垂直二等分線上にあるから、\(C(a,2)\)とおける。
また、\(AC^2=PC^2\)より
\(a^2+1^2=(a-t)^2+2^2\)
整理すると
\(2at=t^2+3\)
\(t≠0\)より \(a=\displaystyle\frac{t^2+3}{2t}\)

よって中心の座標は　\((\displaystyle\frac{t^2+3}{2t},2)\)

(2)

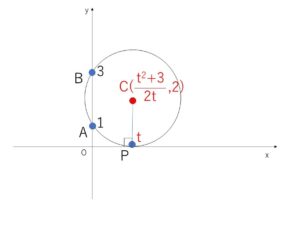
円が\(x\)軸に接するとき点\(P\)が接点となり、\(C,P\)の\(x\)座標は同じになる。

よって
\(\displaystyle\frac{t^2+3}{2t}=t\) より
\(t^2=3\)
\(t>0\) だから \(t=\sqrt{3}\)
このとき \(C(\sqrt{3},2)\)

また円の半径は\(C\)の\(y\)座標と同じで \(2\)

したがって円の方程式は
\((x-\sqrt{3})^2+(y-2)^2=4\)

(3)

(1)(2)の流れに沿って\(A,B\)を通る円を考えると、まず円が\(x\)軸と2点で交わるときは円の内部に\(x\)軸上の点が存在するので、そのような内部の\(x\)軸の点を\(P’\)とすると、\(\angle APB\)\(<\angle AP’B\)
よって円の内部に\(x\)軸上の点がないようなときを考えると、それは円が\(x\)軸と接するときであり、このときは接点\(P\)以外の\(x\)軸上の正の部分にある点\(P’\)は円の外部にあるので、\(\angle APB>\angle AP’B\)
したがって、接するときの点\(P\)における \(\angle APB\) が最も大きいことになります。

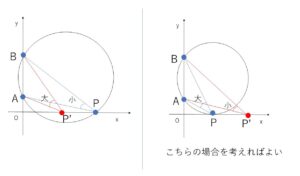
(2)で求めた接する円を考える。
接点\(P\)と、\(P\)以外の\(x\)軸の正の部分にある点\(P’\)について
\(P’\)は円の外部にあるので、\(\angle APB>\angle AP’B\)

よって\(\angle APB\)が最大となるような点\(P\)は、接する円の接点であり、
(2)よりその座標は \((\sqrt{3},0)\)

※円周上の点\(P\)、内部の点\(R\)、外部の点\(Q\)と角の大小について

円周上に定まった点\(A,B\)があり、図の直線\(AB\)より上側の部分について考えると
円周上の点\(P\)、内部の点\(R\)、外部の点\(Q\)において次のことが成り立ちます。

\(\angle ARB>\angle APB\)(円周角)\(>\angle AQB\)

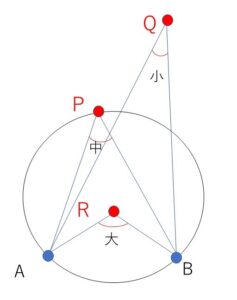
(証明)

(三角形の2つの内角の和=外角 の等式を用います)

\(\angle ARB>\angle APB\)について

図において、円周角の定理により \(\angle APB=\angle AP_0B\)・・・①

また、\(△RP_0B\)において内角と外角を考えると
\(\angle AP_0B+\angle P_0BR=\angle ARB\)
\(\angle P_0BR>0\) より　\(\angle AP_0B\)\(<\angle ARB\)・・・②

①②より \(\angle ARB>\angle APB\)

\(\angle APB\)\(>\angle AQB\)について

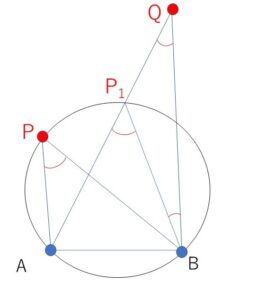
さきほど同様に、図において円周角の定理から \(\angle APB=\angle AP_1B\)・・・③

また、\(△P_1QB\)において2つの内角の和と外角は等しいので
\(\angle AQB+\angle P_1BQ=\angle AP_1B\)
\(\angle P_1BQ>0\) より \(\angle AQB<\angle AP_1B\)・・・④

③④より \(\angle APB>\angle AQB\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2次の方程式の表す図形　back→円の方程式①