円の外部の点から引いた2接線の2接点を通る直線について見ていきます。
(例題1)
点\((1,3)\)から、円 \(x^2+y^2=5\) に引いた2本の接線の2つの接点を結ぶ直線の方程式を求めよ。
としても答えはでますが、もう少しスマートな解法があります。
その解法は、まずは2つの接点の座標を設定するところから始めます。
(解答)
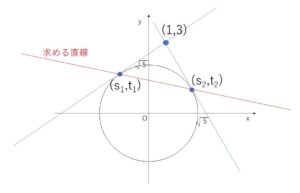
2接点を\((s_1,t_1)\), \((s_2,t_2)\) とおくと2接線は
\(s_1x+t_1y=5\), \(s_2x+t_2y=5\)
これらの接線は \((1,3)\)を通るので
\(1\)\(s_1\)\(+3\)\(t_1\)\(=5\)・・・① \(1\)\(s_2\)\(+3\)\(t_2\)\(=5\)・・・②
①②は 直線 \(1x+3y=5\) が 2接点\((s_1,t_1)\), \((s_2,t_2)\)を通ることを表し、また2接点を通る直線は1本しかない。
よって求める直線の方程式は \(x+3y=5\)
このとき、直線\(RS\)を極線(きょくせん)、外部の点\((p,q)\)を極(きょく)とよびます。
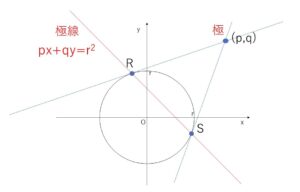
上の例題では、極が\((1,3)\)で、極線が求めた \(x+3y=5\) となっています。
(例題2)
\(a>b>0\) とする。円 \(x^2+y^2=a^2\) の点 \((b,\sqrt{a^2-b^2})\) における接線と\(x\)軸の交点を\(P\)とする。また、円の外部の点 \((b,c)\) からこの円に2本の接線を引き、接点を\(Q,R\)とする。このとき、2点\(Q,R\)を通る直線は\(P\)を通ることを示せ。
また、\(P\)の座標も簡単に出せます。
これらから直線\(QR\)上に\(P\)があることを示します。
(解答)
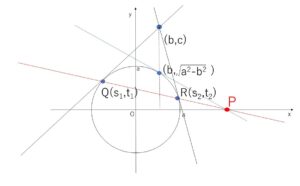
\((b,\sqrt{a^2-b^2})\) における接線の方程式は
\(bx+\sqrt{a^2-b^2}y=a^2\)
よって\(P\)の\(x\)座標は \(y=0\)とすると、\(x=\displaystyle\frac{a^2}{b}\)
ゆえに \(P(\displaystyle\frac{a^2}{b},0)\)
また、\((b,c)\)から引いた2本の接線の2接点\(Q,R\)を\((s_1,t_1)\), \((s_2,t_2)\) とおくと2接線の方程式は
\(s_1x+t_1y=a^2\), \(s_2x+t_2y=a^2\)
これらの接線は \((b,c)\)を通るので
\(bs_1+ct_1=a^2\)・・・① \(bs_2+ct_2=a^2\)・・・②
①②は \(bx+cy=a^2\) が2接点 \((s_1,t_1)\), \((s_2,t_2)\) を通ることを表していて、2接点を通る直線は1本しかないので、\(bx+cy=a^2\)が\(Q,R\)を通る直線の方程式となる。
\(bx+cy=a^2\)・・・③ に \(x=\displaystyle\frac{a^2}{b}\),\(y=0\) を代入すると成り立つので、③は\(P\)を通る。
したがって\(QR\)を通る直線は\(P\)を通る。
(1)\(bx+cy=a^2\) が \((s_1,t_1)\) を通る。
(2)\(s_1x+t_1y=a^2\) が\((b,c)\) を通る。
と2通りの考え方をしているところがポイントです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→弦・接線の長さ back→円の接線の方程式③