弦・接線の長さ

円の弦の長さや接線の一部の長さに関する問題について見ていきます。

(例題)
(1)円 \(x^2+y^2=25\) と点\(A(7,1)\)について、\(A\)から円に引いた接線の接点を\(T\)とするとき、線分\(AT\)の長さを求めよ。
(2)円 \((x-3)^2+(y-2)^2=26\) が直線 \(y=\displaystyle\frac{3}{2}x+k\) を切り取ってできる弦の長さが\(\sqrt{52}\)であるとき、\(k\)の値を求めよ。また、そのときの弦の中点の座標を求めよ。

(解答)
(1)

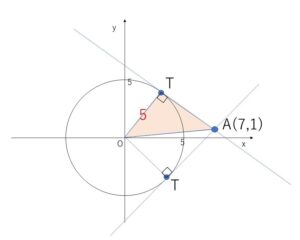
図より、\(OT=5\), \(OA=\sqrt{7^2+1^2}=\sqrt{50}\)
\(△OTA\)は直角三角形なので三平方の定理より
\(AT=\sqrt{OA^2-OT^2}\)\(=\sqrt{50-25}\)\(=\)\(5\)

(2)

同様に図形的に考えます。
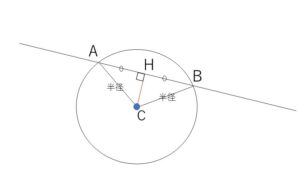
円と直線の交点を\(A,B\)として、円の中心\(C\)から弦に垂線\(CH\)を下すと、\(H\)は線分\(AB\)の中点で、
(弦の半分の長さ)\(=HA\)\(=\sqrt{CA^2-CH^2}\)
(\(HA^2+CH^2=CA^2\))
が成り立ちます。\(CA\)は半径で、\(CH\)は点\(C\)と直線の距離より簡単に求まります。

円 \((x-3)^2+(y-2)^2=26\)  直線 \(3x-2y+2k=0\)・・・① について

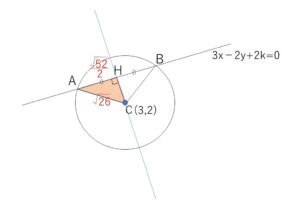
円と直線の交点を\(A,B\)として、円の中心\(C\)から直線に垂線\(CH\)をおろす。
このとき\(H\)は線分\(AB\)の中点となるので、\(AH\)の長さは弦の長さの半分。

円の中心\(C\)は \((3,2)\)だから、直線①と点\(C\)の距離を考えて
\(CH=\displaystyle\frac{|9-4+2k|}{\sqrt{3^2+2^2}}\)\(=\displaystyle\frac{|2k+5|}{\sqrt{13}}\)

弦の半分の長さは \(\displaystyle\frac{\sqrt{52}}{2}\)で、円の半径は\(\sqrt{26}\) だから三平方の定理より
\((\displaystyle\frac{\sqrt{52}}{2})^2+(\displaystyle\frac{|2k+5|}{\sqrt{13}})^2\)\(=(\sqrt{26})^2\)
よって
\((2k+5)^2=13・13\)
\(2k+5=±13\) より
\(k=4,-9\)

また、直線\(CH\)の傾きは \(-\displaystyle\frac{2}{3}\) だから、その方程式は
\(y-2=-\displaystyle\frac{2}{3}(x-3)\)
よって \(2x+3y=12\)・・・②

①②の交点が\(H\)であり、①②を連立して解くと
\(x=\displaystyle\frac{24-6k}{13}\)

\(k=4\) のとき \(x=0\)　②より \(y=4\)
\(k=-9\) のとき　\(x=6\) 　②より \(y=0\)

したがって
\(k=4\)のとき \((0,4)\),　\(k=-9\)のとき \((6,0)\)

(別解)

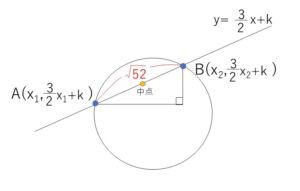
円 \((x-3)^2+(y-2)^2=26\)・・・(ア) と 直線 \(y=\displaystyle\frac{3}{2}x+k\)・・・(イ) について、
その交点\(A,B\)の\(x\)座標を\(x_1,x_2\) (\(x_1<x_2\))とおくと
\(A(x_1,\displaystyle\frac{3}{2}x_1+k)\),　\(B(x_2,\displaystyle\frac{3}{2}x_2+k)\)

(イ)を(ア)に代入して
\((x-3)^2+(\displaystyle\frac{3}{2}x+k-2)^2=26\)
\(x\)について整理して
\(\displaystyle\frac{13}{4}x^2+3(k-4)x\)\(+k^2-4k-13\)\(=0\)・・・(ウ)

(ウ)の2解が\(x_1,x_2\)であり、判別式を\(D\)とすると
\(D=\{3(k-4)\}^2-13(k^2-4k-13)\)\(=-4k^2-20k+313\)\(>0\)・・・(エ)

弦の長さが\(\sqrt{52}\)なので、\(AB\)の長さが\(\sqrt{52}\)より
\(52=(x_2-x_1)^2+\{(\displaystyle\frac{3}{2}x_2+k)-(\displaystyle\frac{3}{2}x_1+k)\}^2\)
よって
\(52=\displaystyle\frac{13}{4}(x_2-x_1)^2\)・・・(オ)

ここで、解の公式より(ウ)を解くと
\(x_2-x_1\)
\(=\displaystyle\frac{-3(k-4)+\sqrt{D}}{2\cdot\displaystyle\frac{13}{4}}-\displaystyle\frac{-3(k-4)-\sqrt{D}}{2\cdot\displaystyle\frac{13}{4}}\)
\(=\displaystyle\frac{4}{13}\sqrt{D}\)

(オ)に代入して
\(52=\displaystyle\frac{13}{4}・\displaystyle\frac{4^2}{13^2}D\)
よって \(169=D\)　(このとき\(D>0\)を満たす)
\(-4k^2-20k+313=169\)
\(k^2+5k-36=0\)
\((k+9)(k-4)=0\) より
\(k=-9,4\)

また、中点の\(x\)座標は、\(x=\displaystyle\frac{x_1+x_2}{2}\) であり
(ウ)と解と係数の関係から
\(x=\displaystyle\frac{x_1+x_2}{2}\)\(=\displaystyle\frac{1}{2}・\displaystyle\frac{-3(k-4)}{\displaystyle\frac{13}{4}}\)\(=\displaystyle\frac{-6(k-4)}{13}\)
\(y\)座標は(イ)より
\(y=\displaystyle\frac{3}{2}x+k\)

よって中点の座標について
\(k=-9\) のとき、\(x=6\),\(y=0\)
\(k=4\) のとき \(x=0\), \(y=4\)

したがって
\(k=-9\)のとき \((6,0)\),　\(k=4\)のとき \((0,4)\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2円の位置関係　back→円の2接点を通る直線(極線)