軌跡の方程式により図形が求まったときに、その図形上の点が条件を満たすことの確認をしなければならない理由について見ていきます。
次の例題を通して逆の確認の意味について考えていきます。
点\(A(1,0)\),\(B(-1,0)\) がある。\(\angle APB=90°\)となる点\(P\)の軌跡を求めよ。
(誤った解法)
\(P(x,y)\) とおく。
\(\angle APB=90°\)・・・① なので
三平方の定理より \(AP^2+BP^2=AB^2\)・・・②
よって
\((x-1)^2+y^2+(x+1)^2+y^2=2^2\)
整理して
\(x^2+y^2=1\)
よって求める軌跡は
円 \(x^2+y^2=1\) ???
当たり前の話かもしれませんが、求まった軌跡上の点の一部でももとの条件を満たしていないときは、もとの条件に反しているわけなのでそれは答えの軌跡とはいえません。
図を描いてみると、円 \(x^2+y^2=1\) 上の点のうち、ほとんどの点は \(\angle APB=90°\) を満たしますが、\((1,0)\)と\((-1,0)\)の2点に関しては \(\angle APB=90°\) とはなりません(角度が作れない)。なのでこれらを除外してやらないといけません。
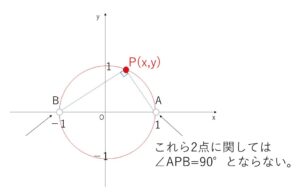
よって正しい答えは 円 \(x^2+y^2=1\) のうち \(A(1,0)\),\(B(-1,0)\)を除いた部分 となるわけですが、どうして単純に出てきた \(x^2+y^2=1\) が答えとならず、もとの条件に合わない点を考えなければならないのでしょうか。
実は、誤った解法で示した方法で求まった \(x^2+y^2=1\) という式は必要条件であって、十分条件ではないからです。つまり 「\(P(x,y)\)が\(x^2+y^2=1\) 上にあれば 、\(\angle APB=90°\) 」が必ずしも成り立たないということです。反例は除いた2点 \((1,0)\)と\((-1,0)\)です。(ただ必要条件なので、「\(\angle APB=90°\) ならば \(x^2+y^2=1\) 上に点\(P\)がある」は成り立っています)
この原因は解法の①②のところです。「①ならば②」という命題は成り立たっていますが、その逆の「②ならば①」という命題は成り立っていません。「②ならば①」の反例がまさに先ほど除外した\((1,0)\)と\((-1,0)\)の2点です。(その他の数式変形は同値変形なので気にすべき所はありません。)
もちろん出てきた軌跡の答えが十分条件(かつ必要条件)である場合もあるので、その場合は除外する点が無いわけですが、一般的には十分条件であるとは限りません。
なので、基本的には逆の確認(十分性の確認)をしなければならないことになります。
以上のことを踏まえると、条件を満たす点\(P\)の軌跡が図形\(F\)であることを示すには次のことを証明することになります。
(2) 図形\(F\)上の任意の点\(P\)は、その条件を満たす。(十分条件)
上の例だと、(1)は成り立っていて、(2)が成り立たない2点があるのでそれを除外したものが完全な答えとなっているわけです。
なお問題を解くにあたって自然に論理を進めると(1)はほとんど成り立つので、
その逆の(2)が成り立つことに注意をすることになります。
最後に、前回扱った例題を改めて考えてみます。
(問題)
2点\(A(-2,0)\),\(B(4,0)\)に対して、\(AP:BP=2:1\) を満たす点\(P\)の軌跡を求めよ。
(解答)
\(P(x,y)\)とおくと、条件より
\(AP=2BP\)
\(AP>0\), \(BP>0\) より
\(AP^2=4BP^2\)
よって
\((x+2)^2+y^2\)\(=4\{(x-4)^2+y^2\}\)
整理すると
\(x^2-12x+y^2+20=0\)
\((x-6)^2+y^2=16\)・・・(A)
したがって条件を満たす任意の点\(P\)は(A)上にある。
次に逆について考えてみます。
(A) \(⇔\)\(AP^2=4BP^2\) は同値の式変形なので
(A)ならば \(AP^2=4BP^2\) が成り立ち、\(AP>0\), \(BP>0\) より
\(AP=2BP\)
ゆえに(A)上にある任意の点\(P\)は 条件\(AP=2BP\) を満たすことになります。
答 円 \((x-6)^2+y^2=4^2\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→動点に対する軌跡 back→軌跡の基礎(アポロニウスの円)