弦の中点の軌跡に関する問題について見ていきます。
(例題)
\(s,t\)を \(s<t\) を満たす実数とする。座標平面上の3点 \(A(1,2)\),\(B(s,s^2)\),\(C(t,t^2)\) が一直線上にあるとする。
(1)\(s\)と\(t\)の関係式を求めよ。
(2)線分\(BC\)の中点を\(M(u,v)\)とする。\(u\)と\(v\)の関係式を求めよ。
(3)\(s,t\)が変化するとき、\(v\)の最小値と、そのときの\(u,s,t\)の値を求めよ。
(解答)
(1)
直線\(BC\)の方程式は
\(y-s^2=\displaystyle\frac{s^2-t^2}{s-t}(x-s)\) だから
\(y=(s+t)(x-s)+s^2\)
\(y=(s+t)x-st\)
これが\(A(1,2)\)を通るので
\(2=s+t-st\)・・・①
(2)
\(M(u,v)\)は、\(B(s,s^2)\),\(C(t,t^2)\) の中点だから
\(u=\displaystyle\frac{s+t}{2}\)・・・②
\(v=\displaystyle\frac{s^2+t^2}{2}\)・・・③
②より \(s+t=2u\)・・・④
③より \(v=\displaystyle\frac{1}{2}\{(s+t)^2-2st\}\)
(1)の関係式 \(st=s+t-2\)・・・① と④から
\(st=2u-2\)・・・⑤
よって
\(v\)
\(=\displaystyle\frac{1}{2}\{(2u)^2-2(2u-2)\}\)
\(=2u^2-2u+2\)
(3)
\(s+t=2u\)・・・④ \(st=2u-2\)・・・⑤ から\(s,t\)が実数であるための\(u\)の条件を検討します。(結果として\(u\)はすべての実数をとることになりますが、\(s,t\)の和と積の式④⑤から\(s,t\)が実数をとる\(u\)の条件を必ず確認してください)
よって\(s,t\)が実数であるための\(u\)の条件の検討が必要になりますが、その方法は例のように2次方程式を作成して判別式を調べることになります。
\(s+t=2u\)・・・④ \(st=2u-2\)・・・⑤ より
\(s,t\)が実数であるためには2次方程式
\(X^2-2uX+(2u-2)=0\) の解が実数でなくてはならない。
\(s,t\)は異なる実数なので、
\(\displaystyle\frac{D}{4}>0\)
\(u^2-(2u-2)>0\)
\((u-1)^2+1>0\)
この不等式はすべての実数\(u\)で成り立つので、\(u\)はすべての実数値をとりうる。
(2)より
\(v\)\(=2u^2-2u+2\)\(=2(u-\displaystyle\frac{1}{2})^2+\displaystyle\frac{3}{2}\)
よって\(v\)の最小値は \(u=\displaystyle\frac{1}{2}\) のとき \(\displaystyle\frac{3}{2}\)
このとき
\(s+t=1\), \(st=-1\) だから
\(s,t\) は 2次方程式 \(X^2-X-1=0\) の2解
これを解くと
\(X=\displaystyle\frac{1±\sqrt{5}}{2}\)
\(s<t\)より
\(s=\displaystyle\frac{1-\sqrt{5}}{2}\), \(t=\displaystyle\frac{1+\sqrt{5}}{2}\)
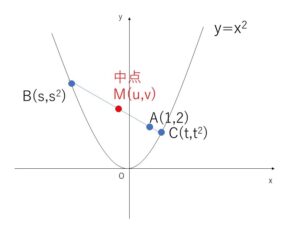
※\(B(s,s^2)\),\(C(t,t^2)\) は 放物線 \(y=x^2\) 上の点であり、図示をしてみると次のようになります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→反転 back→動く2直線の交点の軌跡