今回は、最大最小値を求める関数が分数式である場合や、変数を変換する場合のも問題についてみていきます。
(例題1)
\(x,y\)は実数とし、\(x^2+y^2=36\), \(y≧0\) をみたすとする。このとき
(ア)\(≦\displaystyle\frac{y-3}{x-9}≦\)(イ) である。
今まで通り、\(\displaystyle\frac{y-3}{x-9}=k\) とおいて変形すると \(y=k(x-9)+3\)・・・①
①は傾き\(k\)で\((9,3)\)を通る直線なので、これと半円が共有点をもつ場合について考えていきます。\(k\)を色々変えて直線を動かすと、最小値をとるときは傾き\(k\)が最も小さくなるときなので半円と接するとき、最大値をとるときは傾き\(k\)が最も大きくなるときなので、①が\((6,0)\)を通るときです。
なお、共有点が\(x=9\)(分数式の分母が\(0\)になるとき)とはならないことも断っておきましょう。
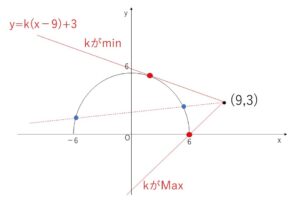
\(x^2+y^2=36\), \(y≧0\) は 原点中心、半径\(6\)の半円を表す。
\(\displaystyle\frac{y-3}{x-9}=k\) とおくと \(y=k(x-9)+3\)・・・①
①と半円が共有点をもつときを考える。(\((9,3)\)は円の外部にある点で共有点とはならない)
①は傾き\(k\),\((9,3)\)を通る直線なので、
\(k\)が最小となるときは①と半円が第1象限で接するときである。
①より \(kx-y-9k+3=0\) だから原点と直線の距離を考えて
\(\displaystyle\frac{|-9k+3|}{\sqrt{k^2+1}}=6\)
\(3|3k-1|=6\sqrt{k^2+1}\)
\(|3k-1|=2\sqrt{k^2+1}\)
両辺正の値なので2乗して
\((3k-1)^2=4(k^2+1)\)
\(5k^2-6k-3=0\) より
\(k=\displaystyle\frac{3±2\sqrt{6}}{5}\)
第1象限で接するとき、\(k<0\) だから
\(k=\displaystyle\frac{3-2\sqrt{6}}{5}\)
次に\(k\)が最大となるときを考えると
傾きが最大となるのは、\((6,0)\)を通るとき。
よって \(k\)\(=\displaystyle\frac{0-3}{6-9}\)\(=1\)
\(\displaystyle\frac{3-2\sqrt{6}}{5}<k<1\) のときも共有点をもつので、これらの値もとりうる。
したがって
(ア)\(\displaystyle\frac{3-2\sqrt{6}}{5}\)\(≦\displaystyle\frac{y-3}{x-9}≦\)(イ)\(1\)
\(y=k(x-9)+3\) を、\(x^2+y^2=36\), \(y≧0\) に代入して
\(x^2+(k(x-9)+3)^2=36\)・・・(A)
\(k(x-9)+3≧0\)・・・(B)
(B)について \(k=0\),\(k≠0\) で場合分けすると、\(k≠0\)のとき
\(x≧-\displaystyle\frac{3}{k}+9\)・・・(B’)
\(x\)が(B’)の範囲のとき、(A)が解をもつ条件を検討することになりますが、範囲にも2次方程式(A)にも文字\(k\)があるのでこれは大変そうです。
(例題2)
実数\(x,y\)が2つの不等式 \(4x+3y≧5\), \(9x+5y≦6\) を同時に満たしているとき、
\((3x+2y)^2+(2x+y)^2\) の最小値を求めよ。
\(13x^2+16xy+5y^2=k\) となりますが、これと不等式で表された領域との共有点を探すのは大変そうです。
そこで、\(3x+2y=X\)・・・②, \(2x+y=Y\)・・・③ とおくと①は \(X^2+Y^2=k\) となり\(XY\)平面上では円を表すことが分かります。あとは\(x,y\)の不等式を\(X,Y\)の不等式にするだけです。②③から連立方程式を解く要領で\(x=X,Yの式\), \(y=X,Yの式\) にして不等式に代入します。
(解答)
\((3x+2y)^2+(2x+y)^2=k\)・・・① とおく。
\(3x+2y=X\)・・・②, \(2x+y=Y\)・・・③ とすると、①は
\(X^2+Y^2=k\)・・・④ (円を表す)
また
③×2-① より
\(x=-X+2Y\)・・・⑤
②×2-②×3 より
\(y=2X-3Y\)・・・⑥
\(4x+3y≧5\), \(9x+5y≦6\) に⑤⑥を代入して
\(4(-X+2Y)+3(2X-3Y)≧5\)
\(9(-X+2Y)+5(2X-3Y)≦6\)
整理して
\(2X-Y≧5\)・・・⑦
\(X+3Y≦6\)・・・⑧
⑦⑧を満たす\(X,Y\)について、\(X^2+Y^2\)の最小値を求めればよい。
⑦⑧の表す領域\(D\)を図示して、\(X^2+Y^2=k\)・・・④ と\(D\)が共有点をもち\(k\)が最小となるときを考える。
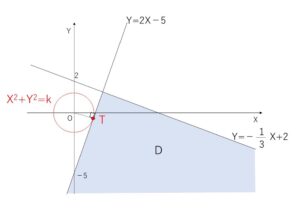
図より \(X^2+Y^2=k\) と \(Y=2X-5\)・・・⑨ が接するとき最小値をとる。
接点を\(T\)とすれば、\(OT\)と⑨は垂直なので、\(OT\)の方程式は
\(y=-\displaystyle\frac{1}{2}X\)・・・⑩
⑨⑩を連立して\(T\)の座標を求めると、\(T(2,-1)\)
よって最小値は
\(k=2^2+(-1)^2=\)\(5\) (\(X=2\), \(Y=-1\))
⑤⑥から
\(x\)\(=-X+2Y=-2-2\)\(=-4\)
\(y\)\(=2X-3Y=4+3\)\(=7\)
答え 最小値 \(5\) (\(x=-4\), \(y=7\)のとき)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→線形計画法(文章問題) back→領域と最大・最小値②(2次式)