弧度法とその利用

新しい角の定義(弧度法)について見ていきます。

 

・弧度法
角度として最初に習い普段使っているものは、「円周を\(360\)等分したときの、弧の中心角の大きさを\(1°\)」とした度数法です(円1周では\(360°\)となる)。
普段当たり前のように使っていますが、そもそもこの\(360\)という数字はどこから出てきたものでしょうか。

約4000年前に、バビロニア人が日が経つにつれて太陽の高度が変わり、1年(365日)でもとの位置に戻ってくることに気づき、太陽が地球の周りを1年かけて周っていると考えました。そこで円周分の角度を\(365°\)としたいところですが、\(360\)のほうが約数が多いために細かい角度を表しやすいように円周分の角度を\(360°\)とし、1日約\(1°\)太陽が動いているということにしたようです。

なので、\(360\)という数字は都合よく決めただけの数字で、絶対的にこの数字にしなければならないというわけではありません。

 

度数法は便利で使いやすいものです。しかし数ⅡBの範囲ではあまり実感がないかもしれませんが、度数法のまま議論を進めると不都合なことがでてきます(数Ⅲ 三角関数の極限、微積分など)。そこで新たに考えられた角の表し方が弧度法です。これは弧の長さに着目した角の表し方です。弧度法では

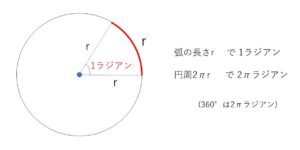
とします。円周は\(2πr\) なので、\(360°\) は弧度法では \(2π\)ラジアン、\(180°\)は \(π\)ラジアンで、半径\(1\)の円の弧の長さがそのまま角に対応しています。

 

1ラジアンは度数法ではどれくらいの角度になるかというと、1ラジアン分の角度を\(α\)とすると円全体との比を考えて

\(r:2πr=α:360°\) より
\(α=\displaystyle\frac{180°}{π}≒\)\(57.3°\)・・・①

です。また①式の左辺と中辺と、1ラジアン\(=α\) より次のことが言えます。

 

よって以下度数法と弧度法の対応関係は次の通りです。なお弧度法では通常「ラジアン」を省略します。

 

・弧度法と扇形の弧の長さ・面積
弧度法を利用して扇形の弧の長さと面積を求めてみます。

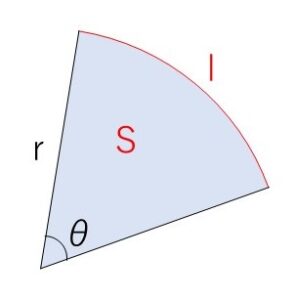
半径\(r\),中心角\(θ\)(ラジアン)の扇形の弧の長さを\(l\)とすると、円全体との比を考えて
\(l:2πr=θ:2π\) より
\(l=rθ\)・・・(A)

扇形の面積\(S\)は同様に
\(S:πr^2=θ:2π\) より
\(S=\displaystyle\frac{1}{2}r^2θ\)・・・(B)
また(A)(B)より
\(S\)\(=\displaystyle\frac{1}{2}r・rθ\)\(=\displaystyle\frac{1}{2}rl\)・・・(C)
とも表せます。

 

 

 

(例題)
(1)\(-420°\)を弧度法で表せ。
(2)弧度法による角\(\displaystyle\frac{8}{5}π\) を度数法で表せ。
(3)半径\(10\),中心角\(120°\)の扇形の弧の長さと面積を求めよ。

 

(解答)
(1)
\(-420×\displaystyle\frac{π}{180}=\)\(-\displaystyle\frac{7}{3}π\)

(2)
\(\displaystyle\frac{8}{5}π×\displaystyle\frac{180}{π}=\)\(288°\)

(3)
弧の長さ\(l\)は
\(l=rθ=10・\displaystyle\frac{2}{3}π=\)\(\displaystyle\frac{20}{3}π\)

面積\(S\)は
\(S=\displaystyle\frac{1}{2}r^2θ=\displaystyle\frac{1}{2}・10^2・\displaystyle\frac{2}{3}π=\)\(\displaystyle\frac{100}{3}π\)

(\(S=\displaystyle\frac{1}{2}rl=\displaystyle\frac{1}{2}・10・\displaystyle\frac{20}{3}π=\)\(\displaystyle\frac{100}{3}π\) でもよい)

 

 

 

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→三角関数の定義　back→一般角