三角関数の相互関係の式について見ていきます。数ⅠAの三角比のときと同じ式が成り立ちます。
・三角関数の相互関係
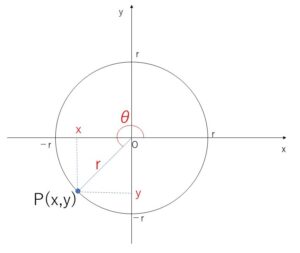
原点中心,半径\(r(≠0)\)の円と角\(θ\)の動径との交点\(P(x,y)\)について、三角関数の定義より
\(\sinθ=\displaystyle\frac{y}{r}\)・・・① \(\cosθ=\displaystyle\frac{x}{r}\)・・・② \(\tanθ=\displaystyle\frac{y}{x}\)・・・③
①②より
\(y=r\sinθ\) \(x=r\cosθ\)
\(\cosθ≠0\)のとき、③に代入して
\(\tanθ\)\(=\displaystyle\frac{r\sinθ}{r\cosθ}\)\(=\displaystyle\frac{\sinθ}{\cosθ}\)・・・(A)
また、\(P(x,y)\)が円\(x^2+y^2=r^2\) 上にあることから
\(r^2\cos^2θ+r^2\sin^2θ=r^2\)
両辺\(r^2\)で割ると
\(\sin^2θ+\cos^2θ=1\)・・・(B)
\(\cosθ≠0\)のとき、(B)の両辺を\(\cos^2θ\)で割ると
\(\tan^2θ+1=\displaystyle\frac{1}{\cos^2θ}\)・・・(C)
\(\sin^2θ+\cos^2θ=1\)・・・(B)
\(\tan^2θ+1=\displaystyle\frac{1}{\cos^2θ}\)・・・(C)
ただし(A)(C)については \(θ≠\displaystyle\frac{π}{2}+nπ\) (\(n\)は整数)
(例題)
(1)\(θ\)が第4象限の角で、\(\tanθ=-2\)のとき、\(\sinθ,\cosθ\)の値を求めよ。
(2)\(\sinθ=\displaystyle\frac{2}{3}\)のとき、\(\cosθ,\tanθ\)の値を求めよ。
(解答)
(1)
\(\tan^2θ+1=\displaystyle\frac{1}{\cos^2θ}\) より
\((-2)^2+1=\displaystyle\frac{1}{\cos^2θ}\)
\(\cos^2θ=\displaystyle\frac{1}{5}\)
\(θ\)は第4象限の角なので、\(\cosθ>0\) より
\(\cosθ=\displaystyle\frac{1}{\sqrt{5}}\)
また、\(\tanθ\)\(=\displaystyle\frac{\sinθ}{\cosθ}\) より \(\sinθ=\tanθ\cosθ\) だから
\(\sinθ\)\(=(-2)・\displaystyle\frac{1}{\sqrt{5}}\)\(=-\displaystyle\frac{2}{\sqrt{5}}\)
(2)
\(\sin^2θ+\cos^2θ=1\) より
\((\displaystyle\frac{2}{3})^2+\cos^2θ=1\)
\(\cos^2θ=\displaystyle\frac{5}{9}\)
単位円を考えると\(\sinθ=y\) なので、\(y=\displaystyle\frac{2}{3}\)となる円上の点は2つあることからも分かります。
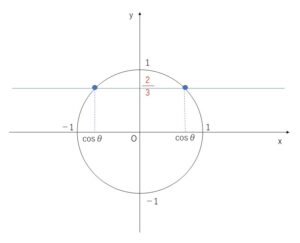
よって \(\cosθ=±\displaystyle\frac{\sqrt{5}}{3}\)
また、\(\tanθ\)\(=\displaystyle\frac{\sinθ}{\cosθ}\) より
\(\tanθ\)\(=\displaystyle\frac{\displaystyle\frac{2}{3}}{±\displaystyle\frac{\sqrt{5}}{3}}\)\(=\displaystyle\frac{\displaystyle\frac{2}{3}×3}{±\displaystyle\frac{\sqrt{5}}{3}×3}\)\(=±\displaystyle\frac{2}{\sqrt{5}}\)
答 \((\cosθ,\tanθ)\)\(=(\displaystyle\frac{\sqrt{5}}{3},\displaystyle\frac{2}{\sqrt{5}})\)\(,(-\displaystyle\frac{\sqrt{5}}{3},-\displaystyle\frac{2}{\sqrt{5}})\) (複号同順)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の相互関係② back→三角関数の定義