引き続き加法定理を利用する問題を見ていきます。
(例題1)
実数\(α,β,γ\) が \(0<α<\displaystyle\frac{π}{2}\), \(0<β<\displaystyle\frac{π}{2}\), \(0<γ<\displaystyle\frac{π}{2}\), \(α+β+γ=\displaystyle\frac{π}{2}\) を満たすとき、
\(\tanα\tanβ\)\(+\tanβ\tanγ\)\(+\tanγ\tanα\)
の値は一定であることを示せ。
(解答)
\(γ=\displaystyle\frac{π}{2}-(α+β)\) なので、
\(\tanγ=\tan\{\displaystyle\frac{π}{2}-(α+β)\}\)\(=\displaystyle\frac{1}{\tan(α+β)}\) です。
\(\tan(α+β)\)について、\(\tan\)が定義できなかったり、\(0\)になることがないことも念のため記載しておきます。(\(α+β≠0,\displaystyle\frac{π}{2}\))
条件から
\(γ=\displaystyle\frac{π}{2}-(α+β)\)・・・①
\(0<γ<\displaystyle\frac{π}{2}\)より、\(0<α+β<\displaystyle\frac{π}{2}\)
よって\(α+β≠0,\displaystyle\frac{π}{2}\) だから①より
\(\tanγ=\tan\{\displaystyle\frac{π}{2}-(α+β)\}\)\(=\displaystyle\frac{1}{\tan(α+β)}\)
したがって
\(\tanα\tanβ\)\(+\tanβ\tanγ\)\(+\tanγ\tanα\)
\(=\)\(\tanα\tanβ\)\(+\tanβ・\displaystyle\frac{1}{\tan(α+β)}\)\(+\displaystyle\frac{1}{\tan(α+β)}・\tanα\)
\(=\)\(\tanα\tanβ\)\(+\displaystyle\frac{\tanα+\tanβ}{\tan(α+β)}\)
\(=\)\(\tanα\tanβ\)\(+(\tanα+\tanβ)・\displaystyle\frac{1-\tanα\tanβ}{\tanα+\tanβ}\)
\(=\)\(\tanα\tanβ\)\(+1-\tanα\tanβ\)
\(=1=\)(一定)
(例題2)
\(\tanθ_1=1\), \(\tanθ_2=\displaystyle\frac{1}{2}\), \(\tanθ_3=\displaystyle\frac{1}{3}\), \(0<θ_i<\displaystyle\frac{π}{2}\) (\(i=1,2,3\)) とするとき、
\(\sin(θ_1+θ_2+θ_3)\) の値を求めよ。
次に\(θ_2+θ_3\) を求めるために、\(\tan(θ_2+θ_3)\) を計算します。
この方法だと早いですが、\(\tan(θ_2+θ_3)\) がキレイな値にならないときしか解けないので別解もあわせて紹介します。
(解法1)
\(\tanθ_1=1\), \(0<θ_1<\displaystyle\frac{π}{2}\) より
\(θ_1=\displaystyle\frac{π}{4}\)
また
\(\tan(θ_2+θ_3)\)\(=\displaystyle\frac{\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}}{1-\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{3}}\)\(=\displaystyle\frac{\displaystyle\frac{5}{6}}{\displaystyle\frac{5}{6}}\)\(=1\)
\(0<θ_2<\displaystyle\frac{π}{2}\), \(0<θ_3<\displaystyle\frac{π}{2}\) より
\(0<θ_2+θ_3<π\) だから
\(θ_2+θ_3=\displaystyle\frac{π}{4}\)
したがって
\(θ_1+θ_2+θ_3=\displaystyle\frac{π}{4}+\displaystyle\frac{π}{4}\)\(=\displaystyle\frac{π}{2}\) であるから
\(\sin(θ_1+θ_2+θ_3)\)
\(=\sin(\displaystyle\frac{π}{2})\)
\(=\)\(1\)
(解法2)
\(θ_1=\displaystyle\frac{π}{4}\) は分かっているので
\(\sin\{θ_1+(θ_2+θ_3)\}\)とみて加法定理を使います。
\(\sin\{θ_1+(θ_2+θ_3)\}\)
\(=\sinθ_1\cos(θ_2+θ_3)\)\(+\cosθ_1\sin(θ_2+θ_3)\)・・・(A)
\(\tanθ_1=1\), \(0<θ_1<\displaystyle\frac{π}{2}\) より
\(θ_1=\displaystyle\frac{π}{4}\)
よって、\(\sinθ_1=\displaystyle\frac{1}{\sqrt{2}}\), \(\cosθ_1=\displaystyle\frac{1}{\sqrt{2}}\)
また、\(\displaystyle\frac{1}{\cos^2θ}=\tan^2θ+1\) より
\(\cos^2θ_2=\displaystyle\frac{4}{5}\)
\(0<θ_2<\displaystyle\frac{π}{2}\) より
\(\cosθ_2=\displaystyle\frac{2}{\sqrt{5}}\)
\(\sin^2θ=1-\cos^2θ\) より
\(\sin^2θ_2=\displaystyle\frac{1}{5}\)
\(0<θ_2<\displaystyle\frac{π}{2}\) より
\(\sinθ_2=\displaystyle\frac{1}{\sqrt{5}}\)
同様に \(\cosθ_3\), \(\sinθ_3\) を求めると
\(\cosθ_3=\displaystyle\frac{3}{\sqrt{10}}\), \(\sinθ_3=\displaystyle\frac{1}{\sqrt{10}}\)
したがって
\(\cos(θ_2+θ_3)\)
\(=\displaystyle\frac{2}{\sqrt{5}}・\displaystyle\frac{3}{\sqrt{10}}\)\(-\displaystyle\frac{1}{\sqrt{5}}・\displaystyle\frac{1}{\sqrt{10}}\)
\(=\displaystyle\frac{1}{\sqrt{2}}\)
\(\sin(θ_2+θ_3)\)
\(=\displaystyle\frac{1}{\sqrt{5}}・\displaystyle\frac{3}{\sqrt{10}}\)\(+\displaystyle\frac{2}{\sqrt{5}}・\displaystyle\frac{1}{\sqrt{10}}\)
\(=\displaystyle\frac{1}{\sqrt{2}}\)
ゆえに(A)より
\(\sin(θ_1+θ_2+θ_3)\)
\(=\displaystyle\frac{1}{\sqrt{2}}・\displaystyle\frac{1}{\sqrt{2}}\)\(+\displaystyle\frac{1}{\sqrt{2}}・\displaystyle\frac{1}{\sqrt{2}}\)
\(=\)\(1\)
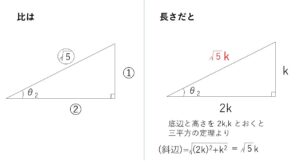
「(底辺):(高さ):(斜辺)\(=2:1:\sqrt{5}\)」
これから、\(\sinθ_2=\displaystyle\frac{1}{\sqrt{5}}\), \(\cosθ_2=\displaystyle\frac{2}{\sqrt{5}}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2直線のなす角 back→加法定理②