今回からは三角関数の最大最小に関する問題について見ていきます。
三角関数の性質や公式をフル活用していくことになりますが、新しい知識はほとんど必要ありません。各問題において、どの公式を使えばいいかということに重点をおいてみてください。
(例題)
(1)\(y=2\sin(θ+\displaystyle\frac{π}{3})\) (\(0≦θ≦\displaystyle\frac{π}{2}\)) の最大値と最小値を求めよ。
(2)\(F=\displaystyle\frac{\sin(θ+30°)-\sin(θ-30°)}{\sin(θ+60°)}\)
(\(30°≦θ≦60°\)) の最大値・最小値を求めよ。
(3)\(0<x<\displaystyle\frac{π}{2}\), \(0<y<\displaystyle\frac{π}{2}\) とする。
\(\tan x\tan y=\displaystyle\frac{1}{2}\)のとき
\(\tan(x+y)+\tan(x-y)\) の最小値を求めよ。
①三角関数の種類の統一 ②角の統一
です。これを目指して式変形していきます。
(解答)
(1)
大丈夫だと思いますが、加法定理を使ったりしないように。すでに\(\sin\)のみの関数にまとめられているので、そのまま考えます。
\(0≦θ≦\displaystyle\frac{π}{2}\) より
\(\displaystyle\frac{π}{3}≦θ+\displaystyle\frac{π}{3}≦\displaystyle\frac{5π}{6}\)
したがって
\(y=2\sin(θ+\displaystyle\frac{π}{3})\) の
最大値は \(θ+\displaystyle\frac{π}{3}=\displaystyle\frac{π}{2}\) のとき \(y=2\)
最小値は \(θ+\displaystyle\frac{π}{3}=\displaystyle\frac{5π}{6}\) のとき \(y=2・\displaystyle\frac{1}{2}=1\)
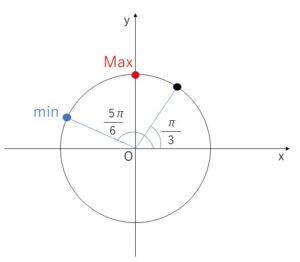
最大値 \(2\) (\(θ=\displaystyle\frac{π}{6}\))
最小値 \(1\) (\(θ=\displaystyle\frac{π}{2}\))
(2)
\(\sin(θ±30°)\)
\(=\sinθ\cdot\displaystyle\frac{\sqrt{3}}{2}±\cosθ\cdot\displaystyle\frac{1}{2}\)
より
\(\sin(θ+30°)-\sin(θ-30°)\)
\(=\cosθ\)
また
\(\sin(θ+60°)\)
\(=\sinθ\cdot\displaystyle\frac{1}{2}+\cosθ\cdot\displaystyle\frac{\sqrt{3}}{2}\)
より
\(F=\displaystyle\frac{\sin(θ+30°)-\sin(θ-30°)}{\sin(θ+60°)}\)
\(=\displaystyle\frac{\cosθ}{\displaystyle\frac{1}{2}\sinθ+\displaystyle\frac{\sqrt{3}}{2}\cosθ}\)
ちなみに分母だけを合成しても意味がありません。そもそも加法定理によって変形をしたので合成したらもとに戻るだけです(合成は加法定理の逆の操作)。
分母分子を2倍して、\(30°≦θ≦60°\) より、\(\cosθ(≠0)\)で分母分子を割ると
\(F=\displaystyle\frac{2}{\tanθ+\sqrt{3}}\)
ここで、\(30°≦θ≦60°\) より
\(\displaystyle\frac{4\sqrt{3}}{3}≦\tanθ+\sqrt{3}≦2\sqrt{3}\)
よって
分母,分子が正の値であることから
\(F\) は \(\tanθ+\sqrt{3}\)が最小値をとるとき最大となり
最大値 \(F=\displaystyle\frac{3・2}{4\sqrt{3}}\)\(=\displaystyle\frac{\sqrt{3}}{2}\) (\(θ=30°\))
最小値は \(\tanθ+\sqrt{3}\)が最大値をとるときで
最小値 \(F=\displaystyle\frac{2}{2\sqrt{3}}\)\(=\displaystyle\frac{\sqrt{3}}{3}\) (\(θ=60°\))
(3)
加法定理と \(\tan x\tan y=\displaystyle\frac{1}{2}\) より
\(\tan(x+y)+\tan(x-y)\)
\(=\displaystyle\frac{\tan x+\tan y}{1-\tan x\tan y}\)\(+\displaystyle\frac{\tan x-\tan y}{1+\tan x\tan y}\)
\(=\displaystyle\frac{\tan x+\tan y}{1-\displaystyle\frac{1}{2}}\)\(+\displaystyle\frac{\tan x-\tan y}{1+\displaystyle\frac{1}{2}}\)
\(=2(\tan x+\tan y)+\displaystyle\frac{2}{3}(\tan x-\tan y)\)
\(=\displaystyle\frac{8}{3}\tan x+\displaystyle\frac{4}{3}\tan y\)
\(\displaystyle\frac{8}{3}\tan x+\displaystyle\frac{4}{3}\tan y\) の最小値がどうなるかということですが、\(x,y\)の範囲から \(\tan x,\tan y\)がともに正なので相加相乗平均を使います。本問は最小値だけを求める問題なのでこれで構いませんが、最大値も求める場合などは文字消去など別の方法に頼ることになります。なおこの問題では\(x,y\)を\(\displaystyle\frac{π}{2}\) に近づければいくらでも大きくなるので最大値はないことになります。
ここで、\(0<x<\displaystyle\frac{π}{2}\), \(0<y<\displaystyle\frac{π}{2}\) より
\(\tan x>0\), \(\tan y>0\) となるので、相加相乗平均の不等式から
\(\displaystyle\frac{8}{3}\tan x+\displaystyle\frac{4}{3}\tan y\)
\(≧2\sqrt{\displaystyle\frac{8}{3}\tan x\cdot\displaystyle\frac{4}{3}\tan y}\)
\(=2\sqrt{\displaystyle\frac{8}{3}\cdot\displaystyle\frac{4}{3}\cdot\displaystyle\frac{1}{2}}\)
\(=\displaystyle\frac{8}{3}\)
等号は
\(\displaystyle\frac{8}{3}\tan x=\displaystyle\frac{4}{3}\tan y\)
つまり
\(2\tan x=\tan y\)
のとき成り立ち
\(\tan x\tan y=\displaystyle\frac{1}{2}\) より
\(\tan x\cdot2\tan x=\displaystyle\frac{1}{2}\)
\(\tan^2x=\displaystyle\frac{1}{4}\)
\(\tan x>0\) より
\(\tan x=\displaystyle\frac{1}{2}\)
このとき \(\tan y=1\)
したがって 最小値は \(\displaystyle\frac{8}{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の最大最小②(2次関数型) back→チェビシェフの多項式