2次関数に帰着できる三角関数の最大最小問題について見ていきます。
(例題1)
関数 \(f(x)=\cos2x+\sin x\) の最小値と最大値を求めよ。
(解答)
\(\cos2x+\sin x\)
\(=-2\sin^2x+\sin x+1\)・・・①
\(\sin x=t\) とおくと、\(-1≦t≦1\) で
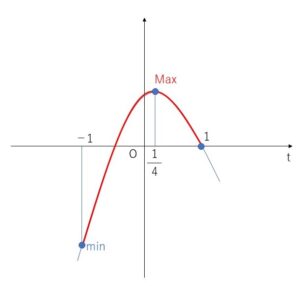
①\(=-2t^2+t+1\)
\(=-2(t-\displaystyle\frac{1}{4})^2+\displaystyle\frac{9}{8}\)
よって
最小値は \(t=-1\) のとき \(-2\)
最大値は \(t=\displaystyle\frac{1}{4}\) のとき \(\displaystyle\frac{9}{8}\)
(例題2)
関数 \(f(x)=a\sin x-\cos^2x+3\) (\(-90°≦x≦90°\)) の最小値が \(-3\) となるような正の定数\(a\)の値を求めよ。
(解答)
\(f(x)\)
\(=a\sin x-(1-\sin^2x)+3\)
\(=\sin^2x+a\sin x+2\)・・・②
\(\sin x=t\) とおくと (\(-90°≦x≦90°\)) より
\(-1≦t≦1\) で
②\(=g(t)\)
\(=t^2+at+2\)
\(=(t+\displaystyle\frac{a}{2})^2-\displaystyle\frac{a^2}{4}+2\)
\(a>0\) より、軸 \(-\displaystyle\frac{a}{2}\) は負の領域にあるので、\(-1\)が境目です。
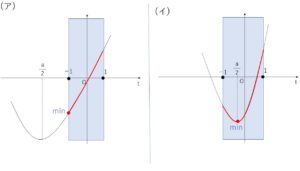
(ア)\(-\displaystyle\frac{a}{2}<-1\) (\(a>2\)) のとき
最小値は \(t=-1\) のときで
\(g(-1)=-a+3\)
\(-a+3=-3\) を解いて
\(a=6\) (\(a>2\)を満たす)
(イ)\(-1≦-\displaystyle\frac{a}{2}<0\) (\(0<a≦2\)) のとき
最小値は \(t=-\displaystyle\frac{a}{2}\) のとき
\(g(-\displaystyle\frac{a}{2})=-\displaystyle\frac{a^2}{4}+2\)
\(-\displaystyle\frac{a^2}{4}+2=-3\) を解いて
\(a=±2\sqrt{5}\)
これは \(0<a≦2\) を満たさないので不適
したがって
\(a=6\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の最大最小③(合成型) back→三角関数の最大最小①