今回は立体図形、特に立方体の塗り分けの問題について考えていきます。
ポイントは固定する色の選び方です。
(例題)
立方体の各面に、隣り合った面の色は異なるように、色を塗りたい。ただし、立方体を回転させて一致する塗り方は同じとみなす。
(1)異なる6色をすべて使って塗る方法は何通りあるか。
(2)異なる5色をすべて使って塗る方法は何通りあるか。
(3)異なる4色をすべて使って塗る方法は何通りあるか。
回転できるままだと分かりにくいので、1つの面を上面に固定します。
立方体は対称的な図形なので、どの面(色)も上面に持ってくることができますが、固定する色はなるべく少ない使用回数の色(できれば1回のもの)が望ましいです。1回しか使っていない色を上面に持ってきて、側面の色の配置を円順列で数えることによって、回転しても自分自身にしか重ならないようにします。(重複するものを考えなくてよくする)
ちなみに(1)については順列のところでも扱いました。(→(2-8)立体の色の塗り分け 例題2 参照) こちらに詳しく書いてあるのでよく分からない人は見てください。
立方体は対称的な図形なので、どの面(色)も上面に持ってくることができますが、固定する色はなるべく少ない使用回数の色(できれば1回のもの)が望ましいです。1回しか使っていない色を上面に持ってきて、側面の色の配置を円順列で数えることによって、回転しても自分自身にしか重ならないようにします。(重複するものを考えなくてよくする)
ちなみに(1)については順列のところでも扱いました。(→(2-8)立体の色の塗り分け 例題2 参照) こちらに詳しく書いてあるのでよく分からない人は見てください。
(解答)
(1)使用する6色を、色1,2,3,4,5,6とする。
(1)使用する6色を、色1,2,3,4,5,6とする。
色1を上面に塗り固定すると、下面の塗り方は色2~6の\(5\)(通り)。
残り4色で側面を塗るので、円順列を考えると、\((4-1)!\) (通り)
よって、\(5×(4-1)!=\)\(30\)(通り)
残り4色で側面を塗るので、円順列を考えると、\((4-1)!\) (通り)
よって、\(5×(4-1)!=\)\(30\)(通り)
(2)
使用する5色を、色1,2,3,4,5としたとき、まず2回使う色を1色選びます(\({}_5\mathrm{C}_1\))。
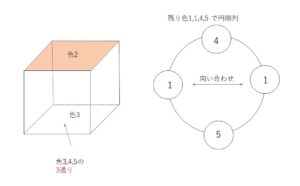
色1を2回使うとして、色1,1,2,3,4,5を6面に塗ります。上面に固定する色は1回しか使わない色、例えば色2にします。下面は色1,1,3,4,5のうち、色1を使うと側面にも色1を使うので隣り合ってしまいます。なので、色3,4,5から例えば3を選びます。あとは残った色1,1,4,5で側面を塗るので、円順列を考えます。
こうして数えた各塗り方は、横方向は円順列を考えているので、横方向の回転では他と一致せず、上面は1回しか使わない色2で固定しているので、上下に回転させても自分自身にしか重なりません。
色1を2回使うとして、色1,1,2,3,4,5を6面に塗ります。上面に固定する色は1回しか使わない色、例えば色2にします。下面は色1,1,3,4,5のうち、色1を使うと側面にも色1を使うので隣り合ってしまいます。なので、色3,4,5から例えば3を選びます。あとは残った色1,1,4,5で側面を塗るので、円順列を考えます。
こうして数えた各塗り方は、横方向は円順列を考えているので、横方向の回転では他と一致せず、上面は1回しか使わない色2で固定しているので、上下に回転させても自分自身にしか重なりません。

使用する5色を、色1,2,3,4,5とする。
まず、2回使う色を選ぶ方法は、\({}_5\mathrm{C}_1\) (通り)
このうち、例えば2回使う色を色1として、6面を色1,1,2,3,4,5 で塗る方法を考える。
色2を一番上面に塗り固定すると、下面は色1で塗ると側面にも色1を使うので隣合う塗り方になってしまい不適。よって下面は色3,4,5の\(3\)通り。
下面を例えば色3で塗ると、側面は色1,1,4,5で塗ることになるが、円順列を考えて色1が隣合わないようにする並べ方は次の図のみの方法で1通り。
まず、2回使う色を選ぶ方法は、\({}_5\mathrm{C}_1\) (通り)
このうち、例えば2回使う色を色1として、6面を色1,1,2,3,4,5 で塗る方法を考える。
色2を一番上面に塗り固定すると、下面は色1で塗ると側面にも色1を使うので隣合う塗り方になってしまい不適。よって下面は色3,4,5の\(3\)通り。
下面を例えば色3で塗ると、側面は色1,1,4,5で塗ることになるが、円順列を考えて色1が隣合わないようにする並べ方は次の図のみの方法で1通り。
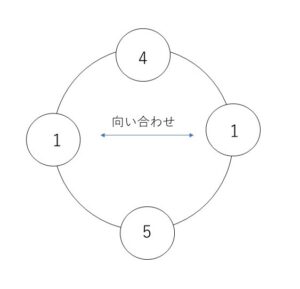
以上より求める塗り方の方法は
\({}_5\mathrm{C}_1×3=\)\(15\)(通り)
\({}_5\mathrm{C}_1×3=\)\(15\)(通り)
ちなみに2回使う色で上面を固定すると、まず5色のうち2回使う色の選び方は、\({}_5\mathrm{C}_1\) 通り。
色1,1,2,3,4,5で塗るとして、上面と下面は色1で塗ることになり、残り色2,3,4,5で側面を塗るので、\((4-1)!\) 通り。ただし次の2つのように回転すると一致するものを重複して考えていて、他の塗り方でもちょうど2個ずつ同じものを数えているので、
\({}_5\mathrm{C}_1×(4-1)!÷2=15\)(通り)
となります。(じゅず順列)
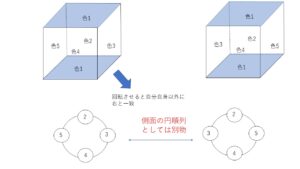
色1,1,2,3,4,5で塗るとして、上面と下面は色1で塗ることになり、残り色2,3,4,5で側面を塗るので、\((4-1)!\) 通り。ただし次の2つのように回転すると一致するものを重複して考えていて、他の塗り方でもちょうど2個ずつ同じものを数えているので、
\({}_5\mathrm{C}_1×(4-1)!÷2=15\)(通り)
となります。(じゅず順列)

上面と下面の色が同じなので、上下に回転させたときに下面が上面に重なるので(上面も下面に重なる)、自分自身以外にも他と重なる可能性があるために、こうした重複が起きてしまいます。
ただ、いつでも重複が起きているわけではなく、円順列が対称的な場合では上下に回転させても自分自身にしか一致しない場合(重複して数えていない)もあります。これについては次回の、→(3-11)同じものを含む円順列・じゅず順列 で扱っていきます。
(3)
使用する色を色1,2,3,4とする。
同じ色を3回使うと、同じ色が隣り合ってしまうため不適。
よって2回使う色が2色あることになるので、この2色の選び方は、\({}_4\mathrm{C}_2=6\) (通り)
このうち、色1,1,2,2,3,4 で6面を塗るとして、上面を色3で塗り固定すると下面は色4で塗ることになる。残り色1,1,2,2で側面を塗ることになるが、同じ色が隣り合わないように円順列を考えると次の図のみで1通り。
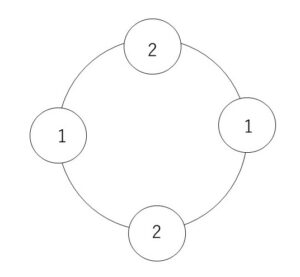
よって、求める塗り方の方法は
\(6×1=\)\(6\)(通り)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。