同じものが複数個ある、円順列・じゅず順列について考えていきます。
ポイントは固定するものを一番数が少ないものを選ぶことです。
(例題)
ガラスでできた玉で、赤色のものが6個、青色のものが2個、透明なものが1個ある。玉には、中心を通って穴が開いているものとする。
(1)これらを1列に並べる方法は何通りあるか。
(2)これらを丸く円形に並べる方法は何通りあるか。
(3)これらの玉に糸を通して首輪をつくる方法は何通りあるか。
(解答)
(1)
ただの同じものを含む順列です。
求める方法は、
\(\displaystyle\frac{9!}{6!2!1!}=\)\(252\)(通り)
\(\displaystyle\frac{9!}{6!2!1!}=\)\(252\)(通り)
(2)
玉の1つを固定して考えます。
(3-9)平面図形の塗り分けと組合せのところでも少し扱いましたが、固定するものは一番数が少ない透明な玉です。1個しかない透明な玉を固定することで、回転しても自分自身にしか重ならないようにします。
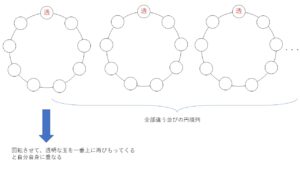
(3-9)平面図形の塗り分けと組合せのところでも少し扱いましたが、固定するものは一番数が少ない透明な玉です。1個しかない透明な玉を固定することで、回転しても自分自身にしか重ならないようにします。

透明な玉を固定すると、残り赤色6個と青色2個の玉を並べる順列を考えて
\(\displaystyle\frac{8!}{6!2!}=\)\(28\)(通り)
\(\displaystyle\frac{8!}{6!2!}=\)\(28\)(通り)
(3)
単純に(2)の28通りを2で割って14通りとはなりません。
もちろん裏返すと他のものと一致するものも28通りの中に含まれていますが、裏返すと他のものと一致せずに、自分自身だけに一致するものもあります。それは円順列での玉の配置が対称的な場合です。例をあげると、次の一番左の配置です。
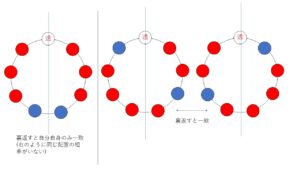
自分自身だけに一致するものは重複して数えていないので(裏返して一致する相手がいない)、2で割る前に28通りからその分を除かないといけません。そして最後に引いた分を足してあげます。
もちろん裏返すと他のものと一致するものも28通りの中に含まれていますが、裏返すと他のものと一致せずに、自分自身だけに一致するものもあります。それは円順列での玉の配置が対称的な場合です。例をあげると、次の一番左の配置です。

自分自身だけに一致するものは重複して数えていないので(裏返して一致する相手がいない)、2で割る前に28通りからその分を除かないといけません。そして最後に引いた分を足してあげます。
対称的な配置の数は、右半分を決めれば左半分も決まるので、赤6個と青2個の半分である赤3個と青1個を右半分に配置し、その場合の数を求めます。
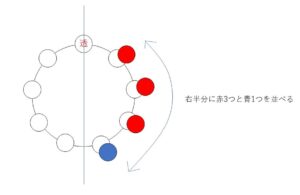

(2)で求めた円順列のうち、裏返して自分自身にしか一致しないものを考える。
そのような場合は対称的に玉が配置される場合で、右半分に赤3個、青1個を配置すれば左半分が決まるので、その総数は、\(\displaystyle\frac{4!}{3!1!}\)\(=4\) (通り)
他の \(28-4\) (通り)の並び方は、裏返すと一致するものがそれぞれ2通りずつあるので、求める首輪を作る方法は、
\((28-4)÷2+4=\)\(16\)(通り)
そのような場合は対称的に玉が配置される場合で、右半分に赤3個、青1個を配置すれば左半分が決まるので、その総数は、\(\displaystyle\frac{4!}{3!1!}\)\(=4\) (通り)
他の \(28-4\) (通り)の並び方は、裏返すと一致するものがそれぞれ2通りずつあるので、求める首輪を作る方法は、
\((28-4)÷2+4=\)\(16\)(通り)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。