組合せの図形に関する問題を何問か見ていきます。
(例題1)
次の図のように、横に4本、縦に5本の直線がいずれも幅1の間隔で並んでいる。これらの直線で囲まれてできる正方形は何個あるか。また、長方形(正方形を含む)は何個あるか。
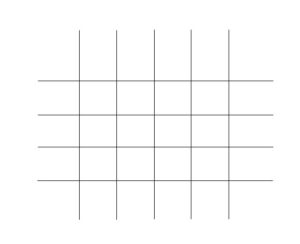
(解答)
正方形の数は例えば1辺の長さが2の場合、横の辺の取り方が①~③の3通り、縦の辺の取り方が①~②の2通りなので、3×2 通りとなります。正方形は他に1辺の長さが1のものと3のものもあるので同様に数えます。
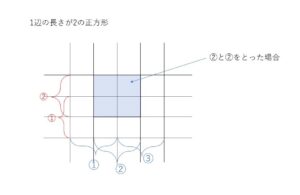

正方形について
(ア)1辺が長さ1の場合
横の辺の取り方が4通りで、縦の辺の取り方が3通り。よって 4×3=12 (通り)
(イ)1辺が長さ2の場合
横の辺の取り方が3通りで、縦の辺の取り方が2通り。よって 3×2=6 (通り)
(ウ)1辺の長さが3の場合
横の辺の取り方が2通りで、縦の辺の取り方が1通り。よって 2×1=2 (通り)
(ア)1辺が長さ1の場合
横の辺の取り方が4通りで、縦の辺の取り方が3通り。よって 4×3=12 (通り)
(イ)1辺が長さ2の場合
横の辺の取り方が3通りで、縦の辺の取り方が2通り。よって 3×2=6 (通り)
(ウ)1辺の長さが3の場合
横の辺の取り方が2通りで、縦の辺の取り方が1通り。よって 2×1=2 (通り)
以上から、正方形の個数は全部で、12+6+2=20(個)
次に長方形は、横2本と縦2本の線分からできているので、横4本の直線から2本選び、縦5本の直線から2本選べば長方形ができます。
長方形について
横の辺の選び方は、4本から2本選ぶので、\({}_4\mathrm{C}_2\) 通り
縦の辺の選び方は、5本から2本選ぶので、\({}_5\mathrm{C}_2\) 通り
よって求める個数は、\({}_4\mathrm{C}_2×{}_5\mathrm{C}_2\)\(=6×10=\)\(60\)(個)
横の辺の選び方は、4本から2本選ぶので、\({}_4\mathrm{C}_2\) 通り
縦の辺の選び方は、5本から2本選ぶので、\({}_5\mathrm{C}_2\) 通り
よって求める個数は、\({}_4\mathrm{C}_2×{}_5\mathrm{C}_2\)\(=6×10=\)\(60\)(個)
ただ2本ずつ直線を選んだだけなので、この60個の中には正方形も含まれています。
(例題2)
図のように、等間隔の3本の平行線と等間隔の4本の平行線が交わっているとき
図のように、等間隔の3本の平行線と等間隔の4本の平行線が交わっているとき
(1)これらの平行線でできる平行四辺形の数を求めよ。
(2)平行線の交点を結んでできる三角形の数を求めよ。
(2)平行線の交点を結んでできる三角形の数を求めよ。
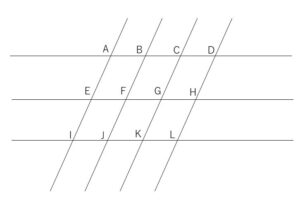
(解答)
(1)
(1)
例題1の長方形の個数と同じように考えることができます。
3本の平行線から2本、4本の平行線から2本選べば平行四辺形が定まるので、
\({}_3\mathrm{C}_2×{}_4\mathrm{C}_2\)\(=3×6=\)\(18\)(個)
\({}_3\mathrm{C}_2×{}_4\mathrm{C}_2\)\(=3×6=\)\(18\)(個)
(2)
同一直線状にない3点を結べば三角形ができますが、3点が同一線上にある場合は3点を結んでも直線にしかならないので、三角形はできません。よって12個の交点から3つ選ぶ総数から三角形ができない場合を除外しなければなりません。さらにこの例題では4点が同一線上にある場合があるので
①4点が同一線上にある場合、4点を結んでできる直線が横の平行線3本
②3点が同一線上にある場合、3点を結んでできる直線が斜めの平行線4本
はすぐに見つかりますが、②の場合はこれだけではありません。
\(AFK\),\(BGL\),\(CFI\),\(DGJ\)も一直線上に並んでいます。(一番小さい平行四辺形の対角線を考える)
①4点が同一線上にある場合、4点を結んでできる直線が横の平行線3本
②3点が同一線上にある場合、3点を結んでできる直線が斜めの平行線4本
はすぐに見つかりますが、②の場合はこれだけではありません。
\(AFK\),\(BGL\),\(CFI\),\(DGJ\)も一直線上に並んでいます。(一番小さい平行四辺形の対角線を考える)
12個の点から3つ選ぶ方法は、\({}_{12}\mathrm{C}_3\) 通り。
このうち選ばれた3点が同一直線上にある場合は三角形ができないので除く。
このうち選ばれた3点が同一直線上にある場合は三角形ができないので除く。
①4点が同一直線上にある場合
4点がのっている直線は全部で3本あり、それぞれの直線について3点の選び方が \({}_4\mathrm{C}_3\) (通り)ある。
②3点が同一直線上にある場合
3点がのっている直線は全部で8本あり、それぞれの直線について3点の選び方は \({}_3\mathrm{C}_3\) (通り)ある。
以上より求める三角形の個数は
\({}_{12}\mathrm{C}_3-(3×{}_4\mathrm{C}_3+8×{}_3\mathrm{C}_3)\)\(=220-(12+8)=\)\(200\)(個)
\({}_{12}\mathrm{C}_3-(3×{}_4\mathrm{C}_3+8×{}_3\mathrm{C}_3)\)\(=220-(12+8)=\)\(200\)(個)
(例題3)
平面上に、4本だけが互いに平行で、どの3本も1点で交わらない10本の直線の交点の個数は全部でいくつあるか。
平面上に、4本だけが互いに平行で、どの3本も1点で交わらない10本の直線の交点の個数は全部でいくつあるか。
どの3本も1点で交わらず、どの2本も平行でない\(n\)本の直線ならば、交点の個数は、2本の直線を選ぶと交点が1つでき、できる交点はそれぞれ別々のものなので\({}_n\mathrm{C}_2\) 個です。ただしこの問題では4本の直線は平行です。平行でない直線なら簡単に個数が求まるので、解答では、まず4本の直線が平行でないとして交点の個数を求めてみて、その総数から実際には平行である4本の直線から2本選んだ場合(交点ができない場合)を除く方針で解いてみます。
(解答)
10本の直線が平行でないとすると、交点は、\({}_{10}\mathrm{C}_2\) (個)できる。
10本の直線が平行でないとすると、交点は、\({}_{10}\mathrm{C}_2\) (個)できる。
実際には、4本の直線が平行なのでこの4本から2本選ぶと交点ができない。
よって求める交点の個数は
\({}_{10}\mathrm{C}_2-{}_4\mathrm{C}_2\)\(=45-6=\)\(39\)(個)
よって求める交点の個数は
\({}_{10}\mathrm{C}_2-{}_4\mathrm{C}_2\)\(=45-6=\)\(39\)(個)
以上になります。お疲れ様でした。
ここまで見ていただきありがとうございました。