微分係数の正負で、関数の増加・減少傾向が分かるので、グラフの形状(主に増減)が分かることになります。今回はそれらに関する、増減表や極値などについて学んでいきます。
(以下しばらくは \(y=f(x)\) は微分可能な関数とする)
・関数の増減
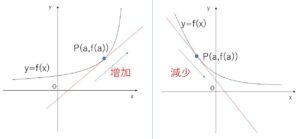
関数 \(y=f(x)\) の \(x=a\) における微分係数 \(f'(a)\) は、この関数の 点\(P(a,f(a))\)における接線の傾きに等しいので
\(f'(a)>0\) ならば 接線は右上がり
\(f'(a)<0\) ならば 接線は右下がり
\(f'(a)=0\) ならば 接線は\(x\)軸に平行
となります。また、接点\(P\)の近くでは、関数 \(y=f(x)\) のグラフの上り下がりは接線の上がり下がりに一致するとみなせるので、
\(f'(a)>0\) ならば \(f(x)\)は \(x=a\) の近くで増加
\(f'(a)<0\) ならば \(f(x)\)は \(x=a\) の近くで減少
\(f'(a)=0\) ならば \(f(x)\)は \(x=a\) の近くで変化しない
ということになります。したがって次のことがいえることになります。
ある区間で
常に \(f'(x)>0\) ならば \(f(x)\)は その区間で単調に増加する。
常に \(f'(x)<0\) ならば \(f(x)\)は その区間で単調に減少する。
常に \(f'(x)=0\) ならば \(f(x)\)は その区間で定数である。
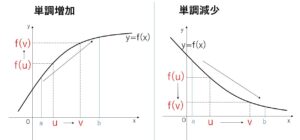
(補足1)単調増加・単調減少の定義
関数 \(y=f(x)\) において、ある区間の任意の \(u,v\) について
\(u<v\) ならば \(f(u)<f(v)\) が成り立つとき
\(f(x)\)はその区間で 単調に増加するといい
\(u<v\) ならば \(f(u)>f(v)\) が成り立つとき
\(f(x)\)はその区間で 単調に減少するといいます。
(補足2)\(f'(x)≧0\), \(f'(x)≦0\) のときの扱い
ある区間で常に\(f'(x)>0\)ならば、\(f(x)\) はその区間で単調に増加していますが、
\(f'(x)≧0\) であっても、\(f'(x)=0\) となる\(x\)が点在しているにすぎない場合では、上記単調増加の条件を満たすので、単調に増加していることになります。
\(f'(x)≦0\) の場合も同様です。
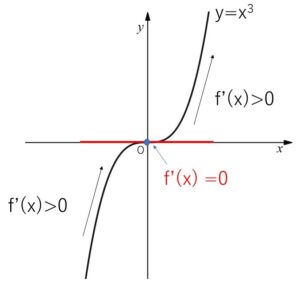
(例)\(f(x)=x^3\)
\(f'(x)=3x^2\) より
\(x=0\) のみ \(f'(x)=0\) 、他は\(f'(x)>0\)
実数全体の \(u,v\)で、\(u<v\) ならば \(f(u)<f(v)\) を満たすので
\(f(x)\)は、実数全体の\(x\)について単調増加となります。
・増減表と極値
\(f'(x)\) の符号でグラフの増減が決定されるので、\(x\)、\(f'(x)\)の符号、\(f(x)\)の増減をまとめて表にするとグラフの増減を分かりやすく表示することができます。このようにまとめた表を増減表とよびます。
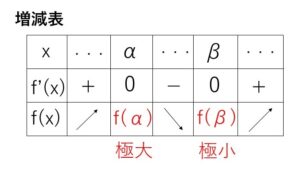
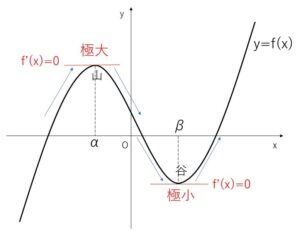
この増減表をもとにグラフを描くと上図のようになり、山になっている部分と、谷になっている部分が存在することになります。
山の部分においては、\(x=α\)を境目にして\(f'(x)\)の符号が正から負に変わり、グラフは増加から減少に変わり、
谷の部分においては、\(x=β\)を境目にして\(f'(x)\)の符号が負から正に変わり、グラフは減少から増加に変化しています。
これらのことを踏まえると一般に
\(x=a\) の前後で \(f'(x)\) の符号が正から負に変わるとき、\(f(x)\)は \(x=a\) を境目に増加から減少に移り変わり、
「\(x=a\) 付近で、\(x≠a\) ならば \(f(x)<f(a)\)」・・・①
が成り立つ、つまり\(x=a\)の近くでは\(f(a)\)が最大となります。そして①が成り立つとき、\(f(x)\) は \(x=a\) で極大になるといい、\(f(a)\) を極大値といいます。
一方、\(x=a\) の前後で \(f'(x)\) の符号が負から正に変わるとき、\(f(x)\)は \(x=a\) を境目に減少から増加に移り変わり、
「\(x=a\) 付近で、\(x≠a\) ならば \(f(x)>f(a)\)」・・・②
が成り立つ、つまり\(x=a\)の近くでは\(f(a)\)が最小となります。そして②が成り立つとき、\(f(x)\) は \(x=a\) で極小になるといい、\(f(a)\) を極小値といいます。
また、極大値と極小値をあわせて極値とよびます。
\(f(a)\)が極値 \(⇔\) \(f'(x)\)は \(x=a\) の前後で符号が変わる
したがって、実際に極値を探すときには、\(f'(a)=0\) になる\(a\)を求めることになりますが、このとき \(x=a\) 前後で符号が変わるとは限らないので、実際に符号が変わっているかどうか確認作業が必要となります。
(例) \(f(x)=x^3\)
\(f'(x)=3x^2=0\) となるのは、\(x=0\)
しかし、\(x=0\) 前後で\(f'(x)\)の符号が変わらないので、\(f(0)\)は極値にはならない。

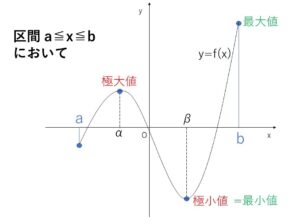
(補足1)最大最小値 と 極大極小値
最大値と極大値、最小値と極小値は異なるものです。極値は部分的にみた最大最小値で、最大最小値は全体としてのものです。もちろん最大値と極大値が一致する(最小値と極小値が一致する)ときもあります。
(補足2)\(f'(a)=0\) と 極値に関する 必要十分性
整式のような微分可能な関数 \(y=f(x)\)で、\(x=a\)で極値をとるとき、\(f'(x)\) は \(x=a\) 前後で符号が変わるので、\(f'(a)=0\) となる。したがって
\(x=a\) で極値となる \(→\) \(f'(a)=0\) (〇)
は成り立つが、反対に \(f'(a)=0\) であっても \(x=a\) 前後で符号が変わるとは限らないので(先述の例 \(f(x)=x^3\) など)
\(f'(a)=0\) \(→\) \(x=a\) で極値となる (×)
は成り立たない。つまり\(f'(a)=0\) は極値となるための必要条件にすぎないから、符号の変化の確認が必要となります。
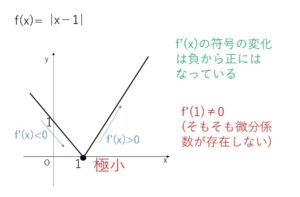
・微分不可能な関数の極値
発展的な内容ですが、極値に関して述べたことは一部で微分が可能でない(微分係数が存在しない)関数では成り立たない場合があります。何種類かそのケースを紹介しておきます。
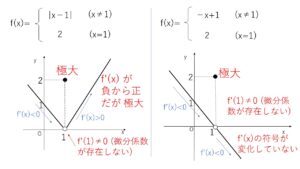
次回は具体的に増減表を作ってグラフを描く演習をしていきます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→関数の増減・極値・グラフ② back→接線のなす角