増減表を作成して、実際にグラフを描いていきます。
(例題)次の関数の極値があればそれを求めて、グラフをかけ。
(1)
① \(y=4x^3-12x^2+9x\)
② \(y=x^3-6x^2+12x-10\)
(2)
③ \(y=3x^4-16x^3+18x^2+5\)
④ \(y=x^4-4x^3\)
また、計算できるなら\(x,y\)切片も求めておきます。
なお(1)は3次関数で、(2)は4次関数です。
(解答)
(1)①
\(f(x)=4x^3-12x^2+9x\) において
\(f'(x)=12x^2-24x+9\)
\(=3(2x-1)(2x-3)\)
\(f'(x)=0\) となる\(x\)は
\(x=\displaystyle\frac{1}{2},\displaystyle\frac{3}{2}\)
\(f(\displaystyle\frac{1}{2})\)
\(=4(\displaystyle\frac{1}{2})^3-12(\displaystyle\frac{1}{2})^2+9(\displaystyle\frac{1}{2})\)
\(=2\)
同様に
\(f(\displaystyle\frac{3}{2})=0\)
また\(x\)軸との交点を求める
\(f(x)=4x^3-12x^2+9x=0\) を解くと
\(x(2x-3)^2=0\) より
\(x=0,\displaystyle\frac{3}{2}\)
以上より増減表とグラフは次の通り。
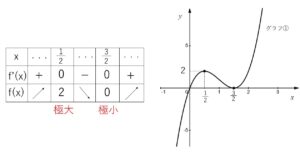
極値は
\(x=\displaystyle\frac{1}{2}\) のとき 極大値 \(2\)
\(x=\displaystyle\frac{3}{2}\) のとき 極小値 \(0\)
(1)②
\(f(x)=x^3-6x^2+12x-10\) において
\(f'(x)=3x^2-12x+12\)
\(=3(x-2)^2\)
\(f'(x)=0\) となるのは
\(x=2\)
増減表とグラフは次の通りで、極値はない。
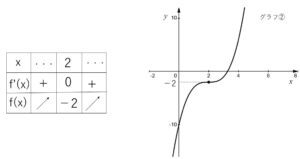
(2)③
\(f(x)=3x^4-16x^3+18x^2+5\) において
\(f'(x)=12x^3-48x^2+36x\)
\(=12x(x-1)(x-3)\)
\(f'(x)=0\) となるのは
\(x=0,1,3\)
増減表とグラフは次の通り
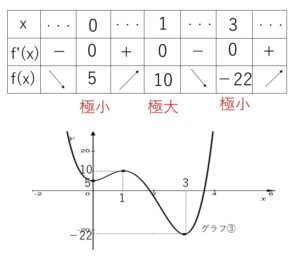
したがって
\(x=0\) のとき 極小値 \(5\)
\(x=3\) のとき 極小値 \(-22\)
\(x=1\) のとき 極大値 \(10\)
(2)④
\(f(x)=x^4-4x^3\) において
\(f'(x)=4x^3-12x^2\)
\(=4x^2(x-3)\)
\(f'(x)=0\) となるのは
\(x=0,3\)
また、\(f(x)=0\) となるのは
\(x^4-4x^3=0\)
\(x^3(x-4)=0\) より
\(x=0,4\)
以上より、増減表とグラフは次の通り
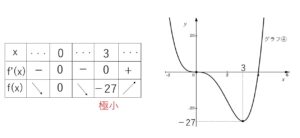
したがって
\(x=3\) のとき 極小値 \(-27\)
また、\(f(3)=-27\) は最小値にもなっています。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→係数決定(極値) back→関数の増減・極値・グラフ①