絶対値を含む関数のグラフや極値に関する問題について見ていきます。
(例題)
(1)関数 \(f(x)=|x|(x^2-5x+3)\) の極値を求めて、グラフの概形をかけ。
(2)関数 \(y=|x^3+2x^2+x+2|\) のグラフをかけ。
(解答)
(1)
(ア) \(x<0\) のとき
\(f(x)=-x(x^2-5x+3)\)
\(=-x^3+5x^2-3x\)
\(f'(x)=-3x^2+10x-3\)
\(=-(3x-1)(x-3)\)
\(x<0\) のとき、\(f'(x)<0\) より
単調減少
(イ) \(x≧0\) のとき
\(f(x)=x(x^2-5x+3)\)
\(=x^3-5x^2+3x\)
\(f'(x)=(3x-1)(x-3)\)
増減表は
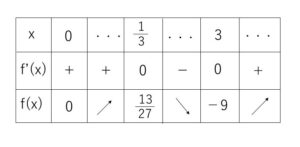
以上からグラフは次の通りで
極小値
\(x=0\) のとき \(0\)
\(x=3\) のとき \(-3\)
極大値
\(x=\displaystyle\frac{1}{3}\) のとき \(\displaystyle\frac{13}{27}\)
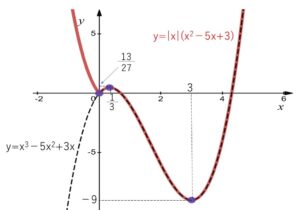
\(f(x)=x^3-5x^2+3x\) のグラフを \(x<0\) の部分だけ\(x\)軸について折り返したもの(符号を変えたもの)を考えてもよいです。(上のグラフ参照)
なお、\(x=0\) では極小値になっていますが、\(x=0\)を場合分けのどちらのケースでも含めるとすると、
左側での微分係数は \(f'(0)=-3\)、右側での微分係数は \(f'(0)=3\) となり異なるので\(x=0\)で微分不可ですが、極小値になっているケースです。
(2)
と因数分解できて容易に場合分けが可能です。
または、\(y=x^3+2x^2+x+2\) のグラフを考えて、負になっている部分だけを\(x\)軸について折り返してもよいです。2個目の解法のほうが場合分けが容易でないケースにも適用できます。
(解答)
\(y=|x^3+2x^2+x+2|=|(x+2)(x^2+1)|\)
(ア) \(x<-2\) のとき
\(y=-x^3-2x^2-x-2\)
\(y’=-3x^2-4x-1\)\(=-(3x+1)(x+1)\)
\(x<-2\) では \(y'<0\) より
単調減少
(イ) \(x≧-2\) のとき
\(y=x^3+2x^2+x+2\)
\(y’=3x^2+4x+1\)\(=(3x+1)(x+1)\)
増減表は
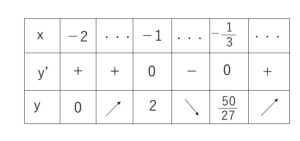
したがってグラフは次の通り
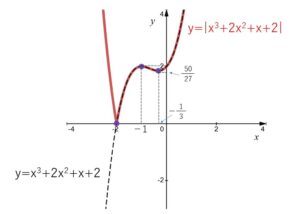
(1)と同様に、\(x=-2\) のときの微分係数は存在しません。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→3次関数のグラフの特徴①(分類) back→係数決定(極値)