3次関数のグラフの形状のパターンについて見ていきます。
・3次関数のグラフまとめ
3次関数
\(y=ax^3+bx^2+cx+d\) (\(a≠0\))
について、まず \(a>0\) の場合について考えていきます。
\(y’=3ax^2+2bx+c\)
より、\(y’=0\) となる 実数\(x\) の個数は判別式によって決定されるので
① \(\displaystyle\frac{D}{4}>0\) つまり \(b^2-3ac>0\) のとき
\(y’=0\) は異なる2つの実数解をもつので、それを \(α,β\) (\(α<β\)) とすると増減は次の通り
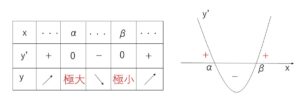
したがって、極大値と極小値を1つずつもち
(極大値)>(極小値) 、 極大値を与える\(x\)の値\(α\)<極小値を与える\(x\)の値\(β\)
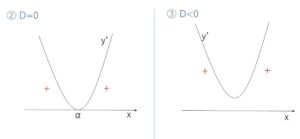
② \(\displaystyle\frac{D}{4}=0\) つまり \(b^2-3ac=0\) のとき
\(y’=0\) は1つの実数解(重解)\(α\)をもち、\(y’≧0\) で、\(y’=0\) となる \(x\)は\(x=α\) のときのみなので単調増加。したがって極値はない。
③ \(\displaystyle\frac{D}{4}<0\) つまり \(b^2-3ac<0\) のとき
\(y’=0\) は実数解をもたず、\(y’>0\)。したがって単調増加で極値はない。
したがってグラフの形状は次のように分類されます。
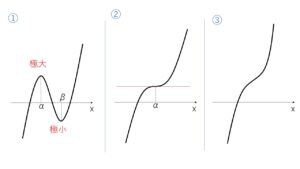
なお \(a<0\) の場合も同様に考えると、上のグラフの左右が逆になったものになります。
・3次方程式の解の個数との関係
先ほど考えたグラフの形状①~③により、3次方程式
\(ax^3+bx^2+cx+d=0\) (\(a≠0\))
の解の個数をグラフの形状で考えることができます。\(a>0\) の場合の分類は次の通りです。(\(a<0\) のときもほぼ同様に考えることができる)
①極値をもつ場合 (\(y’=0\) の2つの実数解を小さい順に \(α,β\) とする)
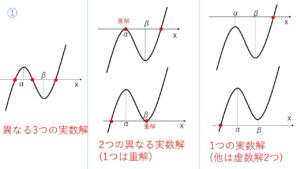
②③極値をもたない場合 (②で \(y’=0\) の実数解(重解)を\(α\)とする)
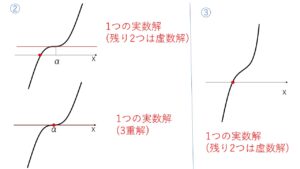
したがってどの場合でも必ず実数解を少なくとも1つもつことなります。
実数係数の3次方程式は、少なくとも1つの実数解をもつ。
(補足)
グラフを考えなくても、3次方程式は重解を含めると解を3つもつことと、実数係数の\(n\)次方程式は虚数解をもてばその共役な複素数も解となることから
(ア)異なる3つの実数解
(イ)異なる2つの実数解(1つは重解)
(ウ)1つの実数解(3重解)
(エ)1つの実数解と2つの虚数解(共役な複素数)
のパターンに分けられることが分かる。
(注)
(ア)~(ウ)で実数解のみもつ場合は網羅されていて、虚数解をもつときはその共役な複素数も解になることに注意すると他に
「異なる2つの虚数解(1つは重解)」の場合も考えられるが、
\((x-α)^2(x-β)=0\)
\((x-α)(実数係数の2次式)=0\) (共役な複素数の和と積は実数になる)
となり、これを展開すると実数係数にならないのでダメです。
次回は3次方程式の重要特徴である対称性について学びます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→3次関数のグラフの特徴②(対称性) back→絶対を含む関数の微分