3次関数のグラフの対称性について見ていきます。
・3次関数のグラフの対称性
3次関数のグラフをいくつか書いていると、なんとなくグラフが対称(点対称)であると気づいた人もいるかもしれませんが、その通りである点について対称になっています。
\(f(x)=ax^3+bx^2+cx+d\) (\(a≠0\)) は、\(y=f(x)\)上の 点\(M(-\displaystyle\frac{b}{3a},f(-\displaystyle\frac{b}{3a}))\) について対称である。特に極値をとる場合、極大値となる座標と極小値となる座標は点\(M\)について対称である。
また、点\(M\) は変曲点であり、点\(M\)の\(x\)座標は、導関数 \(y=f'(x)\) の軸である。
1つ目は\(M\)を原点について平行移動する方法(原点対称が扱いやすいため)、
2つ目は素直に点対称の条件を立式する方法です。
変曲点や導関数の軸についてはあとでまとめて解説します。
(証明1)平行移動の方法
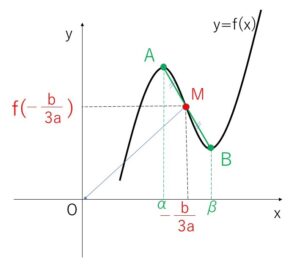
\(y=f(x)=ax^3+bx^2+cx+d\) を、点\(M(-\displaystyle\frac{b}{3a},f(-\displaystyle\frac{b}{3a}))\) が原点にくるように
\(x\)軸方向に \(+\displaystyle\frac{b}{3a}\), \(y\)軸方向に \(-f(-\displaystyle\frac{b}{3a})\)
だけ平行移動すると
\(f(-\displaystyle\frac{b}{3a})=\displaystyle\frac{2b^3}{27a^2}-\displaystyle\frac{bc}{3a}+d\) より
\(y=g(x)=a(x-\displaystyle\frac{b}{3a})^3+b(x-\displaystyle\frac{b}{3a})^2+c(x-\displaystyle\frac{b}{3a})+d\)\(-(\displaystyle\frac{2b^3}{27a^2}-\displaystyle\frac{bc}{3a}+d)\)
(展開して整理すると、\(x^2\)の項と定数項が消えて)
\(g(x)=ax^3+(-\displaystyle\frac{b^2}{3a}+c)x\)
\(g(x)=-g(-x)\) だから、\(y=g(x)\)は原点について対称。
したがって、移動前の \(y=f(x)\) は 点\(M\) について対称となる。
また、\(g'(x)=3ax^2+(-\displaystyle\frac{b^2}{3a}+c)\) より
\(g'(x)=0\) が異なる2つの実数解\(p,q\)をもつとき、つまり極大値と極小値が存在するとき
\(g'(x)=0\) を満たす解は符号が反対なだけなので
\(p=-q\) (極値をとる\(x\)座標は原点対称)
またこれより \(g(p)=-g(q)\) だから、\((p,g(p))\), \((q,g(q))\) は原点対称となるので、移動前の極値どうしも点\(M\)について対称となる。
(証明2)点対称の条件式を立てる
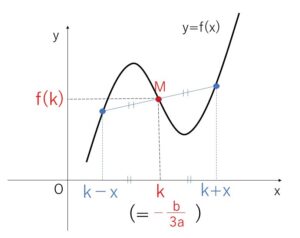
\(y=f(x)=ax^3+bx^2+cx+d\) が 点\((k,f(k))\) について対称
\(⇔\)
すべての\(x\)について \(\displaystyle\frac{f(k-x)+f(k+x)}{2}=f(k)\)・・・① が成り立つ
\(k=-\displaystyle\frac{b}{3a}\) ですが、最後に代入します。
\(f(k-x)=a(k-x)^3+b(k-x)^2+c(k-x)+d\)
\(f(k+x)=a(k+x)^3+b(k+x)^2+c(k+x)+d\)
より
(①の左辺)
\(=ak^3+3kax^2+bk^2+bx^2+ck+d\)
\(=(3ka+b)x^2+ak^3+bk^2+ck+d\)・・・(X)
(\(k=-\displaystyle\frac{b}{3a}\)を1項目だけ代入して)
\(=ak^3+bk^2+ck+d\)
\(=f(k)\)
\(=\)(右辺)
したがって、任意の\(x\)で①が成り立つので、点\((k,f(k))\) つまり 点\(M\) について対称となる。
ここで、極値をもつ場合
\(f'(x)=3ax^2+2bx+c=0\) の異なる2つの実数解を \(α,β\) として
\(α+β=-\displaystyle\frac{2b}{3a}\)
よって
\(2k=(α+β)\)・・・②
\(k+x=β\)・・・③ とすれば、(\(k+x,f(k+x)\)) は極値をとる座標であり、
\(M\)について対称な点については②③より
\(k-x=k+(k-β)=2k-β=(α+β)-β=α\)
したがって、対称な点も極値をとる座標となる。
(※)
\((x,f(x))\) と \((X,f(X))\) を考えて
\(\displaystyle\frac{x+X}{2}=k\)
\(\displaystyle\frac{f(x)+f(X)}{2}=f(k)\)
より、
\(X=2k-x\), \(f(X)=2f(k)-f(x)\)
したがって
\(f(X)=f(2k-x)=2f(k)-f(x)\)
中辺と右辺から
\(\displaystyle\frac{f(2k-x)+f(x)}{2}=f(k)\)
としてもよいです。なおこの式で \(x→x+k\) とすれば①と同じになります。
(変曲点・導関数の軸について)
\(y=f(x)=ax^3+bx^2+cx+d\) について
\(f'(x)=3ax^2+2bx+c\) より
\(y=f'(x)\) の軸は \(x=-\displaystyle\frac{b}{3a}\) であり、これは対称点\(M\)の\(x\)座標と一致している。
また、\(y=f'(x)\) をさらに微分すると
\(f^{\prime\prime}(x)=6ax+2b\)
であり、\(f^{\prime\prime}(x)=0\) を満たす\(x\)、\(x=-\displaystyle\frac{b}{3a}\) とも一致している。
例えば対称点の条件式の立式の場合だと、上記証明の(X)から
\((3ka+b)x^2+f(k)=f(k)\) が任意の\(x\)について成り立つので、
\(k=-\displaystyle\frac{b}{3a}\) という対称の中心が求まります。しかもこれ以外に対称の中心が無いことも示しています。
・3次関数のグラフの等間隔性
簡単のため\(x^3\)の係数が\(1\)とした
\(y=x^3+ax^2+bx+c\)
についてこれが極値をもつとき、この曲線に接する傾きが同じである2本の異なる接線について考えます。
このとき「接点、接線の曲線とのもう1つの交点、点対称の中心」の\(x\)座標は、次のような等間隔の位置関係になります。
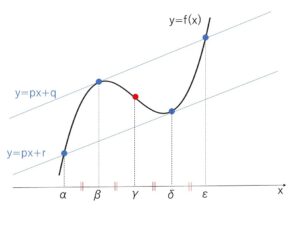
特に接線が\(x\)軸に平行なとき、接点は極値をとるときの座標になり次の通り
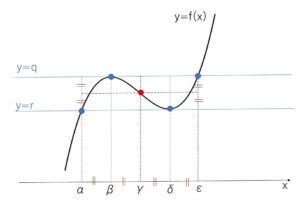
(証明)
\(y=x^3+ax^2+bx+c\) について
点対称の中心は
\(γ=-\displaystyle\frac{a}{3}\)・・・①
また、2つの接線が\(x=β\), \(x=δ\) でそれぞれ接しているので
\(x^3+ax^2+bx+c-(px+q)=(x-β)^2(x-ε)\)
\(x^3+ax^2+bx+c-(px+r)=(x-δ)^2(x-α)\)
\(x^2\) の係数より
\(a=-2β-ε=-2δ-α\)・・・②
①②より
\(γ=\displaystyle\frac{2β+ε}{3}=\displaystyle\frac{2δ+α}{3}\)・・・③
(\(γ\)は、\(β\)から\(ε\) までを\(1:2\)に内分する点
かつ \(α\)から\(δ\) までを\(2:1\)に内分する点 となる)
また
\(y’=3x^2+2ax+b\)
の軸は \(x=-\displaystyle\frac{a}{3}=γ\) であり
2次関数が軸に対称なことと、2つの接線の傾きが等しいことから
\(x=β,δ\) は \(x=γ\) から等距離にあるので
\(γ=\displaystyle\frac{β+δ}{2}\)・・・④
③④より\(α,β,γ,δ,ε\) が等間隔に並ぶことが分かる。
したがって、これらの\(y\)座標も対称の中心から距離が等しくなっています。
なお \(x^3\)の係数が\(1\)でない場合でもほとんど同じように証明できます。
(例題)
\(x\) の関数 \(y=x^3+ax^2+bx+c\) は、\(x=-3\) で極値をとり、そのグラフは点\((-1,3)\) を通り、この点について対称であるという。このとき、\(a,b,c\)の値を求めよ。
(解答1)極値どうしが対称であることを利用する方法
\(f(x)=x^3+ax^2+bx+c\) とおく。
\(f(-1)=3\) より
\(-1+a-b+c=3\)・・・①
また
\(f'(x)=3x^2+2ax+b\) と \(x=-3\) で極値をとることから
\(f'(-3)=0\) より
\(27-6a+b=0\)・・・②
さらに、極値をとる \((-3,y)\) の対称な点 の\(x\)座標を\(p\)とすると
\(\displaystyle\frac{p-3}{2}=-1\) より
\(p=1\)
この対称な点でも 極値となるから
\(f'(1)=0\) より
\(3+2a+b=0\)・・・③
①②③より
\(a=3\), \(b=-9\), \(c=-8\)
まず、\(x=-3\) で極値をとっているか(符号が変化しているかどうか)。
そして、極値しか対称であることを確認していないので、グラフ全体として対称になっているか。
このとき
\(f'(x)=3x^2+6x-9\)\(=3(x+3)(x-1)\)
よって、\(x=-3\) で極値をとる。
そして
\(f(x)=x^3+3x^2-9x-8\) を \((-1,3)\) が原点にくるように平行移動したあとのグラフを\(y=g(x)\) とすると
\(g(x)=(x-1)^3+3(x-1)^2-9(x-1)-8-3\)
\(=x^3-12x\)
となりこれは原点対称。
したがって、移動前の \(y=f(x)\) は \((-1,3)\) について対称となる。
答 \(a=3\), \(b=-9\), \(c=-8\)
(解答2)グラフ全体が点対称であることを利用する方法
\(f(x)=x^3+ax^2+bx+c\) とおく。
\(f'(x)=3x^2+2ax+b\)
\((-1,3)\) を通るから
\(-1+a-b+c=3\)・・・①
\(x=-3\) で極値をとるから
\(27-6a+b=0\)・・・②
また、グラフは \((-1,3)\) について対称だから
\(\displaystyle\frac{f(-1+x)+f(-1-x)}{2}=3\)・・・③
\(f(-1+x)=(x-1)^3+a(x-1)^2+b(x-1)+c\)
\(f(-1-x)=(-x-1)^3+a(-x-1)^2+b(-x-1)+c\)
したがって③は
\((-3+a)x^2+(-1+a-b+c)=3\)
任意の\(x\)について③が成り立つので
\(-3+a=0\)・・・④ (定数項については①と同じ)
①②④より
\(a=3\), \(b=-9\), \(c=-8\)
(以下、\(x=-3\) で 極値をとることの確認をするが省略します)
以上になります。お疲れさまでした。
ここまで見て頂きありがとございました。
next→4次関数のグラフの特徴 back→3次関数のグラフの特徴①(分類)