極値をもつ条件に関する問題について見ていきます。
さらに極小値や極大値と絞られている場合は、負から正・正から負であるかどうかが加わります。
(例題1)
関数 \(f(x)=2x^3+kx^2+kx+1\) について、次の条件を満たすように\(k\)の値の範囲、または\(k\)の値を定めよ。
(1)極値をもたない
(2)\(x=1\) で極値をもつ
(解答)
(1)
\(D=0\) では 1点だけ \(f'(x)=0\) になるところがありますが、この場合も符号の変化(正から負 or 負から正)がないので適することになります。
\(f(x)=2x^3+kx^2+kx+1\) において
\(f'(x)=6x^2+2kx+k\)
極値をもたない条件は \(y=f'(x)\) の2次の係数が正だから
\(y=f'(x)\) が常に\(0\)以上であることである。
したがって、\(f'(x)=0\) の判別式を考えると
\(\displaystyle\frac{D}{4}=k^2-6k≦0\)
\(k(k-6)≦0\)
\(0≦k≦6\)
(2)
また、極小値と限定されているので、この前後で導関数の符号が「負から正」に変わっているか確認します。
\(x=1\) で極小値をとるから
\(f'(1)=0\)
\(6+2k+k=0\)
よって
\(k=-2\)
またこのとき
\(f'(x)=6x^2-4x-2\)
\(=2(3x+1)(x-1)\)
よって \(x=1\) で \(y=f'(x)\) の符号が負から正に変わるので、\(x=1\) で極小値をとる。
以上から
\(k=-2\)
(例題2)
\(f(x)=x^4+4x^3-6ax^2\) が極大値をもつような、定数\(a\)の値の範囲を求めよ。
(解答)
\(f(x)=x^4+4x^3-6ax^2\) において
\(f'(x)=4x^3+12x^2-12ax\)
\(=4x(x^2+3x-3a)\)
\(f'(x)\) は3次関数です。極大値をもつときは「正から負」に符号が変化するところ(グラフが正から負に突き抜けるところ)がある場合ですが、\(f'(x)\) の \(x^3\) の係数が正なので、3次関数のグラフの形状を考えると、3つの異なる実数解をもつときだけが適することになります。
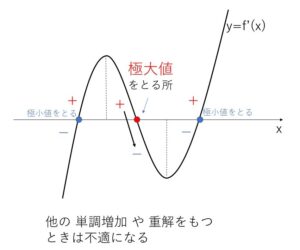
今回の問題では、\(f'(x)=0\) の1つの解が \(x=0\) であることが分かっているので、残りの2次式の部分が、「異なる2つの実数解をもち かつ 解 \(x=0\) をもたない」 ことが条件になります。
\(y=f(x)\) が極大値をもつとき、
\(y=f'(x)\) が正から負に変化する場所があるときで、
\(f'(x)\)の3次の係数が正なので、\(f'(x)=0\) が異なる3つの実数解をもつときを考えればよい。
\(f'(x)=0\) の 1つの解が \(x=0\)だから
\(x^2+3x-3a=0\) が 異なる2つの実数解をもち、かつ それらの解が \(x=0\) でない 時を考えて
\(3^2+12a>0\) かつ \(-3a≠0\)
したがって
\(-\displaystyle\frac{3}{4}<a<0\) , \(a>0\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→極値をとるxの存在範囲 back→極小値と極大値の和・差