微分係数 | 教えて数学理科

微分係数について見ていきます。

数Ⅱで扱ったときと内容は同じです。詳しくは →平均変化率・微分係数を参照してください。ここに書かれていることを簡単にまとめると、グラフの変化を追う際には、異なる2点間(少し離れた2点をイメージ)の変化量を考えますが、さらに精度を上げるために2点を限りなく近づけるという操作をします。

・微分係数(微分の定義)

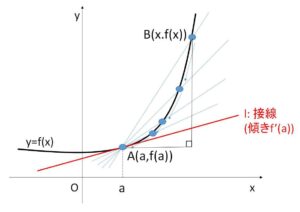
微分係数1

関数\(f(x)\)について、極限値

\(\displaystyle\lim_{x \to a}\displaystyle\frac{f(x)-f(a)}{x-a}\)・・・①　(変化率についての極限値)

が存在するとき、これを\(x=a\)における\(f(x)\)の微分係数といい、\(f'(a)\)で表します。また、このとき\(f(x)\)は \(x=a\) で微分可能といいます。

①において、\(x-a=h\) とおくと

\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)

となるので、\(f(x)\)が\(x=a\)で微分可能であるとき、次の等式が成り立つことなります。

\(f'(a)=\displaystyle\lim_{x \to a}\displaystyle\frac{f(x)-f(a)}{x-a}=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)

なお、\(f'(a)\)は点\(A\)における接線の傾きになります。(接線の定義)

極限値か存在するかどうかは極限値の定義に沿って、右側極限・左側極限を考えます。
両方の極限値が存在して、さらに一致するときに微分可能となります。

(例題)
(1)\(f(x)=\sqrt[3]{x}\) において、\(f'(1)\)を求めよ。

(2)\(f(x)=|x|\) は \(x=0\) で微分可能でないことを示せ。

(解答)
(1)

微分の公式を知っていれば、\(f'(x)=\displaystyle\frac{1}{3}x^{-\frac{2}{3}}\)、\(f'(1)=\displaystyle\frac{1}{3}\)とすぐに計算できますが、最初なので微分の定義から求めていきます。
もちろんこの例題でも右側極限と左側極限が一致するかの確認は必要ですが、計算をしていき最後に \(h \to 0\) (\(x \to 1\)) を考えるときにどちらでも同じことになることは分かります。

\(f'(1)=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(1+h)-f(1)}{h}\)

\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{\sqrt[3]{1+h}-1}{h}\)

(\((a-b)(a^2+ab+b^2)=a^3-b^3\) を利用して有理化すると)

\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{(1+h)-1}{h\{\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1\}}\)

\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{1}{\{\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1\}}\)

\(=\displaystyle\frac{1}{1+1+1}\)

\(=\displaystyle\frac{1}{3}\)

(別解)
\(f'(1)=\displaystyle\lim_{x \to 1}\displaystyle\frac{f(x)-f(1)}{x-1}\)

\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{\sqrt[3]{x}-1}{x-1}\)

(同じく有理化して)

\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{x-1}{(x-1)\{\sqrt[3]{x^2}+\sqrt[3]{x}+1\}}\)

\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{\{\sqrt[3]{x^2}+\sqrt[3]{x}+1\}}\)

\(=\displaystyle\frac{1}{3}\)

(2)

右側極限と左側極限を考えます。
\(x>0\)、\(x<0\) の場合分けで絶対値が外れます。

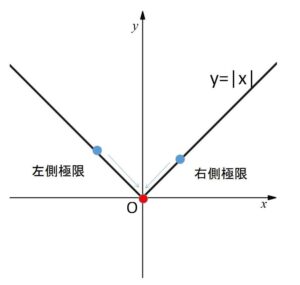
微分係数2

\(f(x)=|x|\)

右側極限について
\(h>0\) のとき \(f(h)=h\) だから

\(\displaystyle\lim_{h \to +0}\displaystyle\frac{f(0+h)-f(0)}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{f(h)}{h}\)
\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{h}{h}\)
\(=\displaystyle\lim_{h \to +0}1\)
\(=1\)

左側極限について
\(h<0\) のとき \(f(h)=-h\) だから

\(\displaystyle\lim_{h \to -0}\displaystyle\frac{f(0+h)-f(0)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{f(h)}{h}\)
\(=\displaystyle\lim_{h \to -0}\displaystyle\frac{-h}{h}\)
\(=\displaystyle\lim_{h \to -0}-1\)
\(=-1\)

したがって極限値　\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(0+h)-f(0)}{h}\)
は存在しないので、微分可能でない。

(参考)
グラフを見ると分かりますが、\(y=|x|\) は \(x=0\) で尖った形をしています。一般的に微分可能なグラフはなめらかな形状をしていて、視覚的にも判断することが可能です。なお、\(x=0\) 以外ではすべての点で微分可能になっています。
この \(y=|x|\) は \(x=0\) で連続ですが、微分が不可能な典型例です。微分可能と連続の関係については次回扱います。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→微分可能と連続①