三角関数などの関数と逆関数の微分

逆関数の導関数に関する例題です。

(例題1)
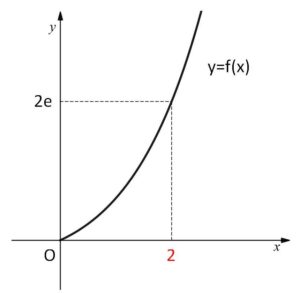
\(x≧0\) で定義される関数 \(f(x)=xe^{\frac{x}{2}}\) は単調増加関数で、逆関数をもつ。この逆関数を\(g(x)\)とし、\(g(x)\)の導関数を\(g'(x)\)とするとき、\(g'(2e)\) を求めよ。

(解答)
逆関数 \(y=g(x)\) の方程式は次のようにも表される。

\(x=ye^{\frac{y}{2}}\)・・・①
\(y\)で微分すると
\(\displaystyle\frac{dx}{dy}=1\cdot e^{\frac{y}{2}}+y\cdot e^{\frac{y}{2}}\cdot\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{e^{\frac{y}{2}}}{2}(2+y)\)

よって
\(y’=\displaystyle\frac{1}{\displaystyle\frac{dx}{dy}}=\displaystyle\frac{2}{e^{\frac{y}{2}}(2+y)}\)

ここで、\(x=2e\) を①に代入すると
\(2e=ye^{\frac{y}{2}}\)・・・②

②の解の1つは \(y=2\) であり、\(f(x)\) の単調増加性により、唯一の解である。

したがって
\(g'(2e)=\displaystyle\frac{2}{e^{\frac{2}{2}}(2+2)}\)

\(=\displaystyle\frac{1}{2e}\)

(参考)
\(f(x)=xe^{\frac{x}{2}}\) (\(x≧0\)) の単調増加性は、この式だけでも分かりますが、
\(f'(x)=\displaystyle\frac{e^{\frac{x}{2}}}{2}(2+x)>0\) からも分かります。

なお、もとの関数 \(y=f(x)\) のグラフは次の通りです。

(例題2)次の関数の逆関数の導関数を\(x\)で表せ。
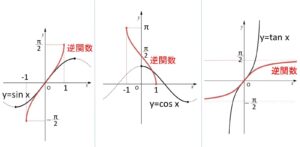
(1)\(f(x)=\sin x\)　(\(-\displaystyle\frac{π}{2}<x<\displaystyle\frac{π}{2}\))

(2)\(g(x)=\cos x\)　(\(0<x<π\))

(3)\(h(x)=\tan x\)　(\(-\displaystyle\frac{π}{2}<x<\displaystyle\frac{π}{2}\))

(1)～(3)の逆関数を
\(f^{-1}(x),\ g^{-1}(x),\ h^{-1}(x)\) とする。

(解答)
(1)
逆関数 \(y=f^{-1}(x)\) の方程式は
\(x=\sin y\)　(\(-\displaystyle\frac{π}{2}<y<\displaystyle\frac{π}{2}\)) ・・・①

両辺を\(y\)で微分して
\(\displaystyle\frac{dx}{dy}=\cos y\)

よって
\(y’=\displaystyle\frac{1}{\cos y}\)

ここで、①より
\(\cos^2y=1-\sin^2y=1-x^2\)
\(-\displaystyle\frac{π}{2}<y<\displaystyle\frac{π}{2}\) より、\(\cos y>0\) だから
\(\cos y=\sqrt{1-x^2}\)

したがって
\(\{f^{-1}(x)\}’=y’=\displaystyle\frac{1}{\sqrt{1-x^2}}\)

(2)
逆関数 \(y=g^{-1}(x)\) の方程式は
\(x=\cos y\)　(\(0<y<π\))・・・②

\(y\)で微分して
\(\displaystyle\frac{dx}{dy}=-\sin y\)

よって
\(y’=-\displaystyle\frac{1}{\sin y}\)

ここで②より
\(\sin^2y=1-\cos^2y=1-x^2\)
\(0<y<π\) だから、\(\sin y>0\)　より
\(\sin y=\sqrt{1-x^2}\)

したがって
\(y’=\{g^{-1}(x)\}’=-\displaystyle\frac{1}{\sqrt{1-x^2}}\)

(3)
逆関数 \(y=h^{-1}(x)\) の方程式は
\(x=\tan y\)　(\(-\displaystyle\frac{π}{2}<x<\displaystyle\frac{π}{2}\))・・・③

\(y\)で微分して③を用いると
\(\displaystyle\frac{dx}{dy}=\displaystyle\frac{1}{\cos^2y}=1+\tan^2y\)

\(=1+x^2\)

したがって
\(y’=\{h^{-1}(x)\}’=\displaystyle\frac{1}{1+x^2}\)

(参考)
\(f(x)=\sin x\) (\(-\displaystyle\frac{π}{2}≦x≦\displaystyle\frac{π}{2}\))

\(g(x)=\cos x\)　(\(0≦x≦π\))

と端点を含めても逆関数は存在しますが、(1)(2)の結果から分かるように、端点を含めると導関数の分母が\(0\)になってしまう、つまり微分係数が存在しないので、省いてあります。

また、通常はこの例題のような範囲について逆関数を考えますが、単調増加(単調減少)の部分を取り出せばよいので、範囲を変えて逆関数を考えることも可能です。この際は導関数が若干変わる場合があります。(符号が変わる)

最後に、この例題の範囲における \(\ \sin x,\ \cos x,\ \tan x\) の逆関数のグラフをもとの関数とともに図示しておきます。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→高次導関数　back→微分可能と連続②