引き続き、文字を含む最大最小値に関する問題です。
今回は区間のほうが文字になってるパターンです。
(例題1)
\(a>0\) とする。
関数 \(y=3x-x^3\) (\(-a≦x≦a\)) の最大値を求めよ。
(解答)
\(y=3x-x^3\) において
\(y’=3(1+x)(1-x)\) より増減表とグラフは次の通り。
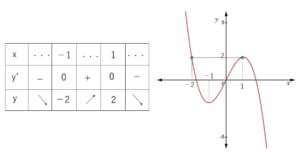
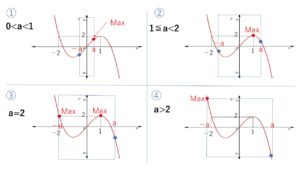
①しばらくは右端が最大
②\(a=1\) からは、右側で極大になるときを含むので、しばらくはこれが最大
③\(a=2\) で右側の極大と、左端が同じになる
④\(a>2\) のときは左端が最大
と推移していきます。解答では③は左端が最大としてもよいので、④とまとめてしまいます。
\(y=2\) となる座標を求めると
\(3x-x^3=2\)
\((x-1)^2(x+2)=0\) より
\(x=-2\)
\(a\)を変化させたときの最大値をグラフから考えると
\(0<a<1\) のとき \(x=a\) で
最大値 \(3a-a^3\)
\(1≦a<2\) のとき \(x=1\) で
最大値 \(2\)
\(a≧2\) のとき \(x=-a\) で
最大値 \(-3a+a^3\)
(例題2)
\(f(x)=2x^3-9x^2+12x-2\) とする。各数\(t\)に対して、区間 \(t≦x≦t+1\) における \(f(x)\) の最大値を表す関数 \(g(t)\) を、\(t\)の値の範囲によって求めよ。
今回の区間は 幅が\(1\) になっていて、\(t\)が変化すると横に動いていきます。
ひとまずグラフを書いて、区間を横に動かして最大値の推移を追いかけます。
(解答)
\(f(x)=2x^3-9x^2+12x-2\) において
\(f'(x)=6(x-1)(x-2)\) より
増減表とグラフは次の通り。
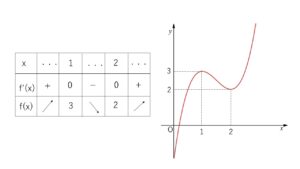
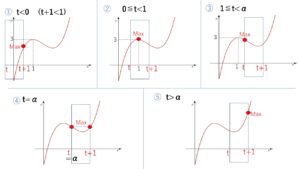
①しばらくは(\(t+1=1\)) までは、右端が最大
②左端が1になるまで(\(t=1\)まで)は、\(x=1\) のとき(極大値のとき)最大
③しばらくは左端が最大
④下に凸の部分なので、ある所で左端と右端が同じなりどちらも最大
⑤以降は右端が最大
と推移していきます。④については簡単に求まらないので、方程式を立ててそのときの\(t\)の値を求めましょう。
また例によって解答では④を右端のときとして⑤に含めます。
幅\(1\)の区間を動かすことにより最大値\(g(t)\)を考えると
①\(t+1<1\) つまり \(t<0\) のとき
右端で最大となるから
\(g(t)\)
\(=f(t+1)\)
\(=2(t+1)^3-9(t+1)^2+12(t+1)-2\)
\(=2t^3-3t^2+3\)
②\(0≦t<1\) のとき
極大値のとき最大で
\(g(t)=f(1)\)\(=3\)
ここで \(t≧1\) のとき
\(f(t)=f(t+1)\) を解くと
\(2t^3-9t^2+12t-2\)\(=2t^3-3t^2+3\)
\(6t^2-12t+5=0\)
\(t=\displaystyle\frac{6±\sqrt{6}}{6}\)
\(t≧1\) だから
\(t=\displaystyle\frac{6+\sqrt{6}}{6}\) (図での\(α\)になる)
③\(1≦t<\displaystyle\frac{6+\sqrt{6}}{6}\) のとき
左端が最大となるから
\(g(t)=f(t)\)\(=2t^3-9t^2+12t-2\)
④\(t≧\displaystyle\frac{6+\sqrt{6}}{6}\) のとき
右端が最大となるから
\(g(t)=f(t+1)\)\(=2t^3-3t^2+3\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→係数決定(最大・最小値) back→最大・最小値①(文字含む)