微分を利用した最大最小値に関する、関数の係数決定の問題について見ていきます。
(例題1)
関数 \(f(x)=x^3+3ax^2\) (\(a>0\)) が、 \(-2≦x≦2\) において最大値\(24\)をもつとき、\(a\)の値を求めよ。
なお本問は、区間が定まっていて関数が変化するタイプになります。
(解答)
\(f(x)=x^3+3ax^2\) \(-2≦x≦2\) において
\(f'(x)=3x(x+2a)\)
\(f'(x)=0\) となるのは
\(x=0,-2a\)
\(x=0\)のほう(極小値のとき)は固定なので、もう一方の \(x=-2a\) のときが、区間 \(-2≦x≦2\) に入るかどうかで場合分けします。
① \(-2<-2a<0\) のとき
つまり \(0<a<1\) のとき
増減表は次の通り。

よって最大値は、
\(f(-2a)=4a^3\)
\(f(2)=8+12a\)
のどちらかになるが、\(0<a<1\) のとき
\(8+12a>8\), \(4a^3<4\) より
\(f(2)>f(-2a)\)
したがって最大値が\(24\)だから
\(8+12a=24\)
\(a=\displaystyle\frac{4}{3}\)
\(0<a<1\) を満たさないので不適。
② \(-2a≦-2\)
つまり \(a≧1\) のとき
増減表は次の通り。
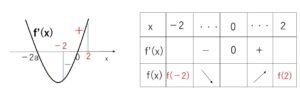
よって最大値は
\(f(-2)=-8+12a\)
\(f(2)=8+12a\)
のどちらかになるが、\(a≧1\) のとき
\(f(2)>f(-2)\) となる。
よって最大値が\(24\)より
\(8+12a=24\)
\(a=\displaystyle\frac{4}{3}\) (\(a≧1\)を満たす)
以上より
\(a=\displaystyle\frac{4}{3}\)
(例題2)
\(a\) を実数の定数とし、\(f(x)=x^3-3ax^2+a\) とする。\(x≦2\) の範囲で \(f(x)\) の最大値が\(105\) となるような\(a\)をすべて求めよ。
(解答)
\(f(x)=x^3-3ax^2+a\) において
\(f'(x)=3x(x-2a)\)
\(f'(x)=0\) となるのは
\(x=0,2a\)
①\(a=0\), ②\(a<0\), ③\(a>0\) で場合分けします。
区間が \(x≦2\) なので、③をさらに \(2a=2\) つまり、\(a=1\)を境目に場合分けします。
① \(a=0\) のとき
\(f(x)=x^3\) であるから、最大値は \(f(2)=8\) となり不適。
② \(a<0\) のとき
増減表は次の通り
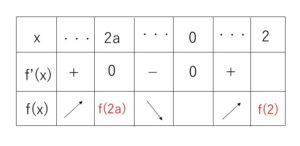
よって最大値は \(f(2a)\) ,\(f(2)\) のどちらかになる。
(ア)\(f(2a)=105\) のとき
\(-4a^3+a=105\)
\((a+3)(4a^2-12a+35)=0\)
\(4a^2-12a+35=0\) の解は虚数解だから
\(a=-3\) (\(a<0\)を満たす)
このとき
\(f(2)=8-11a=41<105\)
となるから適する。
(イ) \(f(2)=105\) のとき
\(8-11a=105\)
\(a=-\displaystyle\frac{97}{11}\)
このとき
\(f(2a)=-4a^3+a=-a(4a^2-1)\)
\(f(2a)=8(4\cdot64-1)\) となるから、\(105\)より大きいです。
ここで、\(a<-8\) だから
\(-a>8\) , \(a^2>64\) であり
\(f(2a)>8(4\cdot64-1)>105\)
となるから不適。
③\(a>0\)のとき
\(0<2a<2\) と \(2a≧2\)
つまり
\(0<a<1\) と \(a≧1\) で場合分けした増減表は次の通り。
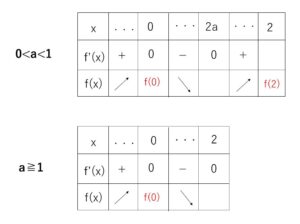
\(0<a<1\) のときは最大値が\(f(0)\)か\(f(2)\)であり、
\(f(0)=a=105\)
\(f(2)=8-11a=105\)
のいずれの場合にも、\(0<a<1\) を満たさず不適。
\(a≧1\) のときは最大値が\(f(0)\)で
\(f(0)=\)\(a=105\) で適する。
以上より
\(a=-3,105\)
\(f(2a)-f(2)=-4a^3+a-(8-11a)=-4(a-1)^2(a+2)\)
より、\(a=-2\)を境目に大小が入れ替わります。そうすると
(ア)\(a=-3\) の場合が適当で、(イ)\(a=-\displaystyle\frac{97}{11}\) のほうが不適であることがすぐに分かります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→他の関数を含む最大・最小値 back→最大・最小値②(文字含む)