三角関数、指数関数、対数関数などを含む関数の最大最小値に関する問題について見ていきます。
(例題1)
関数 \(f(x)=\log_{2}x+2\log_{2}(6-x)\) の最大値を求めよ。
あとは和の形なので真数部分を積にして、真数部分だけに着目すると3次関数になります。
(解答)
真数条件から
\(x>0\) かつ \(6-x>0\)
よって \(0<x<6\)・・・①
\(f(x)=\log_{2}x+2\log_{2}(6-x)\)
\(=\log_{2}x+\log_{2}(6-x)^2\)
\(=\log_{2}x(6-x)^2\)
したがって、\(x(6-x)^2\) の最大値を求めれば、\(f(x)\)の最大値を求めることができます。
ここで
\(g(x)=x(6-x)^2=x^3-12x^2+36x\) とおくと
\(g'(x)=3(x-2)(x-6)\)
①の範囲で増減表は次の通り
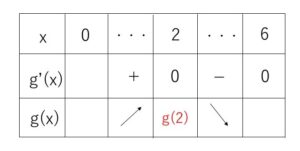
よって、\(g(x)\)の最大値は \(x=2\) のとき
\(g(2)=32\)
したがって対数の底が\(2(>1)\)だから、\(g(x)\)が最大となるとき\(f(x)\)も最大で、その値は
\(f(2)=\log_{2}32=\)\(5\)
答 最大値 \(5\) (\(x=2)\)
(例題2)
2つの関数を
\(t=\cosθ+\sqrt{3}\sinθ\)
\(y=-4\cos3θ+\cos2θ-\sqrt{3}\sin2θ+2\cosθ+2\sqrt{3}\sinθ\)
とする。
(1)\(\cos3θ\) を \(t\) の関数で表せ。
(2)\(y\) を \(t\) の関数で表せ。
(3) \(0°≦θ≦180°\) のとき、\(y\) の最大値、最小値とそのときの \(θ\) の値を求めよ。
(解答)
(1)
\(\cos3θ=4\cos^3θ-3\cosθ\)
と \(\cosθ\) の3次式で表されることから、\(t\)を3乗することを考えます。
これで全然問題ないのですが少し強引な感じもするので、別解法とスッキリとした方法も紹介します。参考にしてください。
\(t^3=(\cosθ+\sqrt{3}\sinθ)^3\)
\(t^3=\cos^3θ+3\sqrt{3}\cos^2θ\sinθ+9\cosθ\sin^2θ+3\sqrt{3}\sin^3θ\)
\(t^3=\cos^3θ+3\sqrt{3}\cos^2θ\sinθ+9\cosθ(1-\cos^2θ)+3\sqrt{3}\sinθ(1-\cos^2θ)\)
\(t^3=-8\cos^3θ+9\cosθ+3\sqrt{3}\sinθ\)
よって
\(4\cos^3θ=-\displaystyle\frac{1}{2}t^3+\displaystyle\frac{9}{2}\cosθ+\displaystyle\frac{3\sqrt{3}}{2}\sinθ\)
\(\cos3θ=4\cos^3θ-3\cosθ\) に代入して
\(\cos3θ=-\displaystyle\frac{1}{2}t^3+\displaystyle\frac{3}{2}\cosθ+\displaystyle\frac{3\sqrt{3}}{2}\sinθ\)
\(=-\displaystyle\frac{1}{2}t^3+\displaystyle\frac{3}{2}(\cosθ+\sqrt{3}\sinθ)\)
\(=-\displaystyle\frac{1}{2}t^3+\displaystyle\frac{3}{2}t\)
(別解)
\(\cos\)の合成は知らない人が多いと思うので、\(\cos(θ-α)\)の加法定理を頭に浮かべながら次のように式変形をするとよいです。
\(t=\cosθ+\sqrt{3}\sinθ\)
\(=2(\cosθ\cdot\displaystyle\frac{1}{2}+\sinθ\cdot\displaystyle\frac{\sqrt{3}}{2})\)
\(=2(\cosθ\cos60°+\sinθ\sin60°)\)
\(=2\cos(θ-60°)\)
よって
\(\cos3θ\)
\(=-\cos(3θ-180°)\)
\(=-\cos3(θ-60°)\)
\(=-4\cos^3(θ-60°)+3\cos(θ-60°)\)
\(=-4(\displaystyle\frac{t}{2})^3+3(\displaystyle\frac{t}{2})\)
\(=-\displaystyle\frac{1}{2}t^3+\displaystyle\frac{3}{2}t\)
(2)
\(\cos2θ-\sqrt{3}\sin2θ\) を\(t\)で表すことを考えます。\(2θ\)は\(\cos,\sin\)の2次式になるので、(1)と同様に今度は\(t\)を2乗します。
\(t^2=(\cosθ+\sqrt{3}\sinθ)^2\)
\(t^2=\cos^2θ+2\sqrt{3}\cosθ\sinθ+3\sin^2θ\)
\(t^2=\displaystyle\frac{1+\cos2θ}{2}+\sqrt{3}\sin2θ+3\cdot\displaystyle\frac{1-\cos2θ}{2}\)
よって
\(\cos2θ-\sqrt{3}\sin2θ=-t^2+2\)
(1)と合わせて
\(y=-4(-\displaystyle\frac{1}{2}t^3+\displaystyle\frac{3}{2}t)+(-t^2+2)+2t\)
\(=2t^3-t^2-4t+2\)
(別解)
(1)の別解と同様の方法だと
\(\cos2θ-\sqrt{3}\sin2θ\)
\(=2\{\cos2θ\cdot\displaystyle\frac{1}{2}+\sin2θ\cdot(-\displaystyle\frac{\sqrt{3}}{2})\}\)
\(=2\{\cos2θ\cos(-60°)+\sin2θ\sin(-60°)\}\)
\(=2\cos(2θ+60°)\)
\(=-2\cos(2θ+60°-180°)\)
\(=-2\cos(2θ-120°)\)
\(=-2\cos2(θ-60°)\)
\(=-2\{2\cos^2(θ-60°)-1\}\)
\(=-2\{2(\displaystyle\frac{1}{2}t)^2-1\}\)
\(=-t^2+2\)
(以下本解答と同様)
(3)
定義域 \(t=\cosθ+\sqrt{3}\sinθ\) の範囲を調べるのを忘れずに。
\(t=\sqrt{3}\sinθ+\cosθ\)
\(=2\sin(θ+30°)\)
\(0°≦θ≦180°\) より
\(30°≦θ+30°≦210°\) だから
\(-1≦t≦2\)・・・①
\(f(t)=2t^3-t^2-4t+2\) とおくと
\(f'(t)=2(3t+2)(t-1)\)
①の範囲で増減表を作ると次の通り。
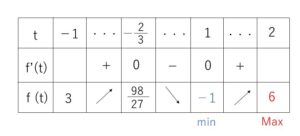
したがって、最大値は\(6\), 最小値は\(-1\)
このときの\(θ\)を求めると
最大値については
\(t=2\sin(θ+30°)=2\) より
\(\sin(θ+30°)=1\)
\(30°≦θ+30°≦210°\) だから
\(θ+30°=90°\)
\(θ=60°\)
最小値については
\(t=2\sin(θ+30°)=1\) より
\(\sin(θ+30°)=\displaystyle\frac{1}{2}\)
\(30°≦θ+30°≦210°\) だから
\(θ+30°=30°,150°\)
\(θ=0°,120°\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→条件付き最大・最小値① back→係数決定(最大・最小値)