速度・加速度の微分による定義について学んでいきます。
微分の定義のときのように、まずはある時間内の平均の速度というざっくりとしたものを考えて、次に時間間隔を極めて短くしていき、瞬間的な速度というものを考えます。
・速度・加速度
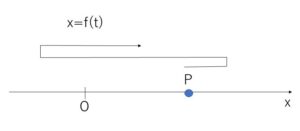
数直線上を運動する点\(P\)の位置\(x\)を、\(t\)の関数で表されるとします。つまり
\(x=f(t)\)
であるとすると、時刻 \(t\) から \(t+Δt\) までの、\(x\)の変化率
\(\bar{v}=\displaystyle\frac{Δx}{Δt}=\displaystyle\frac{f(t+Δt)-f(t)}{Δt}\)
をこの間の点\(P\)の平均速度と呼びます。
そして、この平均速度の \(Δt→0\) とした極限値
\(v=\displaystyle\lim_{Δt→0}\displaystyle\frac{Δx}{Δt}=\displaystyle\lim_{Δt→0}\displaystyle\frac{f(t+Δt)-f(t)}{Δt}=\displaystyle\frac{dx}{dt}\)\(=f'(t)\)
を、時刻\(t\)における点\(P\)の速度といいます(瞬間的な速度)。
変化の仕方によっては速度は正にも負にもなり得り、負の値になるときは数直線の正の方向と逆方向に進んでいることになります。
そこで、速度\(v\)の絶対値\(|v|\)を速さとし、単に速度の大きさのみに着目する場合には速さを扱うことになります。
小中学校でやるような 「(道のり)÷(時間)」は速度が一定な場合の特殊例です。ただし \(x÷t\) という形は類似しています。
我々の日常生活においても速度が一定という状況ももちろんありますが、例えば電車に乗っていて駅に近づけば速度は減少するし、駅につけば止まるし、また発車すれば加速するというように速度は変化します。そこで速度の変化も考えることが重要になってきて、それが加速度というものになります。
さらに、速度 \(v\) の 時刻\(t\)における変化率を考えると、\(v=f'(t)\)だから
\(α=\displaystyle\frac{dv}{dt}\)\(=f^{\prime\prime}(t)\)
を、時刻\(t\)における点\(P\)の加速度といい、絶対値をとった \(|α|\) を加速度の大きさといいます。
(例題1)
直線軌道上を走る電車がブレーキをかけてから、\(t\)秒間に進んだ距離\(x\)メートルは
\(x=30t-0.5t^2\)
であるとする。ブレーキをかけてから何秒後に何メートル進んで停止するか。また、ブレーキをかけてから速度が半減する(速度が\(\displaystyle\frac{1}{2}\)になる)までに何メートル進んだか。
(解答)
速度を\(v\) (m/秒)とすると
\(v=\displaystyle\frac{dx}{dt}=30-t\)
電車が停止するとき、\(v=0\) だから
\(30-t=0\)
\(t=30\) (秒)
このとき進んだ距離は
\(x=30\cdot30-0.5\cdot30^2\)\(=450\) (m)
よって
\(30\)秒後に、\(450\)(m) 進んで停止する。
また、\(t=0\)での速度は\(30\) (m/秒) なので、速度が半減する時間は
\(30-t=\displaystyle\frac{30}{2}\)
\(t=15\)
したがってこの間に進んだ距離は
\(x=30\cdot15-0.5\cdot15^2\)\(=337.5\) (m)
(例題2)
半径\(1\)cmの球型の風船があり、空気を入れはじめてから、半径は毎秒\(0.5\)cmの割合で増加しているという。
(1)\(4\)秒後の体積の増加する速度を求めよ。
(2)\(6\)秒後の表面積の増加する速度を求めよ。
半径が分かれば、\(t\)秒後の体積も表面積も\(t\)で表すことができます。
(解答)
(1)
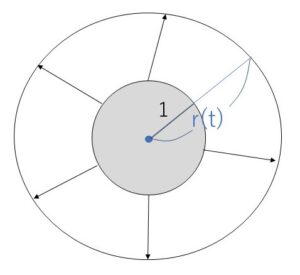
\(t\)秒後の半径を\(r(t)\)とすると
\(r(t)=1+0.5t\) (cm)
\(t\)秒後の体積\(V(t)\)は
\(V(t)=\displaystyle\frac{4}{3}π\{r(t)\}^3=\displaystyle\frac{4}{3}π(1+0.5t)^3\)\(=\displaystyle\frac{1}{6}π\cdot2^3(1+0.5t)^3=\displaystyle\frac{1}{6}π(2+t)^3\)
累乗の微分を使いますが、使いたくない人は展開しても構いません。
\(t\)で微分すると
\(V'(t)=\displaystyle\frac{1}{2}π(2+t)^2\)
よって \(t=4\) 秒後の増加速度は
\(V'(4)=\)\(18π\) (cm\(^3\)/秒)
(2)
\(t\)秒後の表面積\(S(t)\)は
\(S(t)=4π(1+0.5t)^2\)\(=π(2+t)^2\)
\(t\)で微分して
\(S'(t)=2π(2+t)\)
\(t=6\)秒後の表面積の増加速度は
\(S'(6)=\)\(16π\) (cm\(^2\)/秒)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→実数解の個数① back→文章問題(最大・最小値)