文章問題(最大・最小値) | 教えて数学理科

微分を利用する文章問題について見ていきます。

(例題1)
底面の半径 \(r\) 、高さ\(h\)の円錐に、底面が正方形である直方体が図のように内接しているとする。次の問いに答えよ。
(1)直方体の底面の辺の長さを\(x\)とするとき、直方体の体積は\(x\)のどのような関数で表されるか。
(2)直方体の体積の最大値を求めよ。

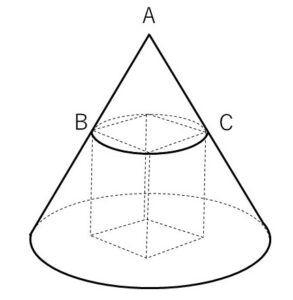
微分　文章題例題1-1

(解答)
(1)

立体の問題の定石は、平面(断面)を考えることです。
円錐の高さ、半径と接点\(B,C\)を含むような、頂点\(A\)と接点\(B,C\)を含む断面を考えます。
直方体の底面積は\(x^2\)なので、あとは高さを\(x\)で表すだけです。

円錐の頂点と、直方体の底面の正方形の対角線を含む断面を考える。

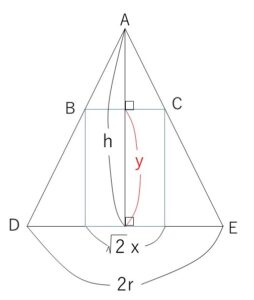
微分文章題例題1-2

高さ\(y\)を\(x\)で表すには、相似の利用が一番早いと思います。
他には三平方の定理などでもできると思います。

直方体の高さを\(y\)として、対角線の長さ\(BC\)は、\(\sqrt{2}x\)で、
\(△ABC\)と\(△ADE\)は相似だから

\((h-y):h=\sqrt{2}x:2r\)

よって
\(y=h-\displaystyle\frac{xh}{\sqrt{2}r}\)

したがって体積\(V(x)\)は
\(V(x)=x^2y\)\(=x^2h(1-\displaystyle\frac{x}{\sqrt{2}r})\)

(2)

微分するだけですが、\(x\)の範囲を考えるのを忘れずに。
断面図を見ると分かりやすいですが、対角線は最大で直径の\(2r\)までしかとれないので、\(\sqrt{2}x<2r\)。あとは辺の長さは正なので \(x>0\)です。
合わせて、\(0<x<\sqrt{2}r\) となり、立体で考えると、\(x=\sqrt{2}r\) のときは、高さが無くなりペシャンコになり、\(x=0\) のときは底面が点になり無くなります(直方体の高さは\(h\)に相当)。

\(x\)の範囲を考えると
\(x>0\) , \(\sqrt{2}x<2r\)
よって
\(0<x<\sqrt{2}r\)・・・①

(1)より
\(V(x)=h(x^2-\displaystyle\frac{x^3}{\sqrt{2}r})\)

\(x\)で微分して
\(V'(x)=hx(2-\displaystyle\frac{3x}{\sqrt{2}r})\)
\(=\displaystyle\frac{3h}{\sqrt{2}r}x(\displaystyle\frac{2\sqrt{2}r}{3}-x)\)

①の範囲で増減表は次の通り。

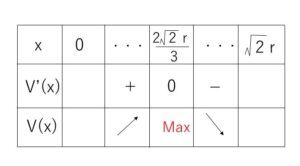
微分文章題例題1-3

したがって最大値は
\(V(\displaystyle\frac{2\sqrt{2}r}{3})\)
\(=h(\displaystyle\frac{2\sqrt{2}r}{3})^2(1-\displaystyle\frac{2\sqrt{2}r}{3}\cdot\displaystyle\frac{1}{\sqrt{2}r})\)
\(=\displaystyle\frac{8}{27}hr^2\)

体積なので次数は辺の長さの3乗です。軽い確認にはなります。

(例題2)
\(a\)を定数とする。辺の長さが\(a\)と\(2a\)の長方形の厚紙がある。この厚紙の四隅から同じ大きさの正方形を切り落とし、ふたのない直方体の容器を作る。容積が最大となるとき、切り落とした正方形の1辺の長さを\(a\)を用いて表せ。また、そのときの容積を求めよ。ただし紙の厚さは容積を求めるときに考慮しないものとする。

切り落とす正方形の一辺を\(x\)として、直方体の体積を\(x\)で表します。
素直な問題ですが、(例題1)と同様\(x\)の範囲に注意です。

(解答)
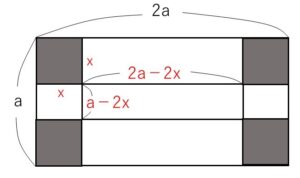
微分文章題例題2-1

切り落とす正方形の1辺を\(x\)とする。

まず、\(x\)の範囲を考えると
\(x>0\), \(a-2x>0\) より
\(0<x<\displaystyle\frac{a}{2}\)・・・①
(このとき、長辺 \(2a-2x\)は正になる)

直方体の容積\(V(x)\)は
\(V(x)=(a-2x)(2a-2x)x\)
\(=4x^3-6ax^2+2a^2x\)

\(V'(x)=2(6x^2-6ax+a^2)\)

\(V'(x)=0\) を満たす\(x\)は
\(x=\displaystyle\frac{3±\sqrt{3}}{6}a\)

\(x=\displaystyle\frac{3}{6}a=\displaystyle\frac{1}{2}a\) なので、平方根が＋のほうは①の範囲外です。

このうち①を満たすのは
\(x=\displaystyle\frac{3-\sqrt{3}}{6}a\)

よって増減表は次の通り。

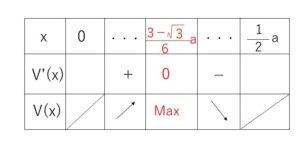
微分文章題例題2-2

\(x=\displaystyle\frac{3-\sqrt{3}}{6}a\) を代入するには、最初の積の形になっているところに代入すると計算しやすいです。

したがって、最大値は
\(V(\displaystyle\frac{3-\sqrt{3}}{6}a)\)
\(=(a-2\cdot\displaystyle\frac{3-\sqrt{3}}{6}a)(2a-2\cdot\displaystyle\frac{3-\sqrt{3}}{6}a)\cdot\displaystyle\frac{3-\sqrt{3}}{6}a\)
\(=\displaystyle\frac{\sqrt{3}}{3}a\cdot\displaystyle\frac{3+\sqrt{3}}{3}a\cdot\displaystyle\frac{3-\sqrt{3}}{6}a\)
\(=\displaystyle\frac{\sqrt{3}}{9}a^3\)

答 1辺の長さ \(\displaystyle\frac{3-\sqrt{3}}{6}a\) のとき最大値 \(\displaystyle\frac{\sqrt{3}}{9}a^3\)

他に複雑な値の代入の際には、\(V(x)\)を、\(V'(x)\)で割った余り(1次式)に着目する方法もあります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→速度・加速度・変化率　 back→条件付き最大・最小値②