引き続き微分を利用した方程式の解の個数の問題を扱っていきます。
→(3-5)3次関数のグラフの特徴 を参考にしてください
(例題1)
\(m\)を実数の定数とする。
3次方程式 \(x^3-3mx^2+m=0\) の異なる実数解の個数を調べよ。
仮に、\(x^3=3mx^2-m\) としても、曲線どうしの交点を考えることになり、これをグラフで視覚化しても複雑です。よって、素直に与式の左辺そのものを\(y=f(x)\) とおいて\(x\)軸との交点の個数を調べます。それと盲点になりやすいかもしれませんが、方程式の解が具体的に求まる場合もあるので、いきなりグラフを考えるのではなく方程式の解を探す作業も最初にしておきましょう。
(解答)
\(f(x)=x^3-3mx^2+m\) とおいて、\(y=f(x)\) と\(x\)軸の交点の個数を調べる
\(f'(x)=3x(x-2m)\)
\(f(x)=0\) となるのは \(x=0,2m\)
(i)\(m=0\) のとき
\(f'(x)=3x^2≧0\) よりグラフは単調増加。
したがって、実数解の個数は 1個
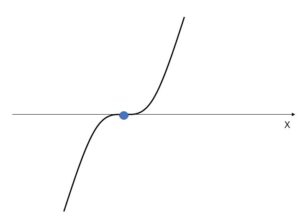
(ii)\(m≠0\) のとき
\(m>0\), \(m<0\) で増減表を考えると次の通り。
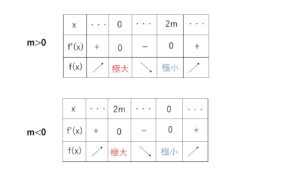
グラフの\(x\)軸との共有点の個数は、2つの極値が\(x\)軸について同じ側か反対側か(符号が同じが違うか)で変わってくるので、極値どうしの積の正負で場合分けします。
ここで、\(m<0\) でも \(m>0\) でも極値をとる\(x\)が違うだけでグラフの形状は同じなので、まとめて扱っていきます。
(a) \(f(0)・f(2m)>0\) のとき
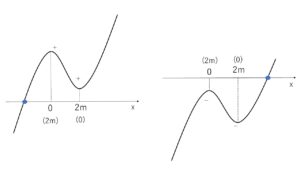
グラフと\(x\)軸の交点は1個だから、実数解は1個
このとき
\(m(-4m^3+m)>0\) より
\(m^2(2m+1)(2m-1)<0\)
\(-\displaystyle\frac{1}{2}<m<\displaystyle\frac{1}{2}\) (\(m≠0\))
(b) \(f(0)・f(2m)=0\) のとき
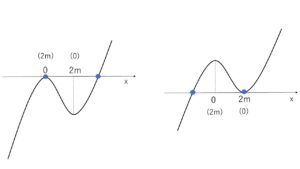
グラフと\(x\)軸の交点は2個だから、実数解は2個
このとき
\(m(-4m^3+m)=0\) より
\(m^2(2m+1)(2m-1)=0\)
\(m≠0\) だから
\(m=±\displaystyle\frac{1}{2}\)
(c)\(f(0)・f(2m)<0\) のとき
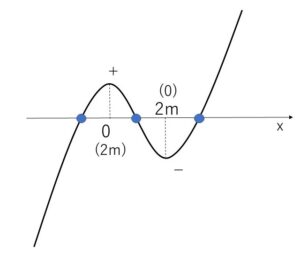
グラフと\(x\)軸の交点は3個だから、実数解は3個
このとき
\(m(-4m^3+m)<0\) より
\(m^2(2m+1)(2m-1)>0\)
\(m<-\displaystyle\frac{1}{2}\), \(m>\displaystyle\frac{1}{2}\)
以上をまとめると
\(-\displaystyle\frac{1}{2}<m<\displaystyle\frac{1}{2}\) のとき 1個
\(m=±\displaystyle\frac{1}{2}\) のとき 2個
\(m<-\displaystyle\frac{1}{2}\), \(m>\displaystyle\frac{1}{2}\) のとき 3個
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線の本数① back→実数解の個数①