引き続き接線の本数に関する問題です。
(例題1)
\(xy\)平面上の 点\((a,b)\) から 曲線 \(y=x^3-x\) に接線がちょうど2本だけ引くことができ、この2本の接線が直交するとき \((a,b)\) を求めよ。
(解答)
\(y=x^3-x\) 上の 点 \((t,t^3-t)\) における接線は
\(y’=3x^2-1\) より
\(y=(3t^2-1)(x-t)+t^3-t\)
整理して
\(y=(3t^2-1)x-2t^3\)
これが \((a,b)\)を通るから
\(b=(3t^2-1)a-2t^3\)
\(t\)について整理すると
\(2t^3-3at^2+a+b=0\)・・・①
\(f(t)=2t^3-3at^2+a+b\) とおくと
\(f'(t)=6t(t-a)\)
\(f'(t)=0\) となるのは \(t=0,a\)
(ア) \(a=0\) のとき
\(f'(t)=6t^2≧0\) より、\(f(t)\)は単調増加になり方程式①の実数解の個数が1個となるから、接線が1本しか存在せず不適。
(イ) \(a≠0\) のとき
\(y=f(t)\) は極大値と極小値を1つずつもち、接線がちょうど2本あるときは方程式①の実数解がちょうど2つ存在するときだから
\(f(0)=0\) または \(f(a)=0\)
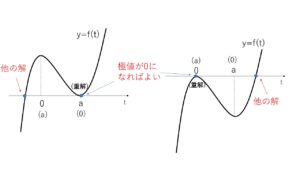
(i) \(f(0)=0\) のとき
①より
\(a+b=0\)
したがって、\(b=-a\)・・・②
②を①に代入して
\(2t^3-3at^2=0\)
\(t^2(2t-3a)=0\) (\(t=0\)は重解)
\(t=0,\displaystyle\frac{3}{2}a\)
これが2つの接線の接点の\(x\)座標になる。
(ii) \(f(a)=0\) のとき
①より
\(-a^3+a+b=0\)
したがって \(b=a^3-a\)・・・③
③を①に代入して
\(2t^3-3at^2+a^3=0\)
\(t=a\)が重解になっていることに注意すると
\((t-a)^2(2t+a)=0\)
\(t=a,-\displaystyle\frac{1}{2}a\)
これが2つの接線の接点の\(x\)座標になる。
(i)について
2つの接線の傾き \(y’=3x^2-1\) より
\(t=0,\displaystyle\frac{3}{2}a\) を代入して
\(y’=-1\), \(y’=\displaystyle\frac{27}{4}a^2-1\) だから
直交するためには
\((-1)(\displaystyle\frac{27}{4}a^2-1)=-1\)
これを解くと
\(a=±\displaystyle\frac{2\sqrt{6}}{9}\)
\(b=-a\)・・・②より
\(a=∓\displaystyle\frac{2\sqrt{6}}{9}\)
(ii)について
2つの接線の傾きは \(y’=3x^2-1\) より
\(t=a,-\displaystyle\frac{1}{2}a\) を代入して
\(y’=3a^2-1\), \(y’=\displaystyle\frac{3}{4}a^2-1\) だから
直交するためには
\((3a^2-1)(\displaystyle\frac{3}{4}a^2-1)=-1\)
整理すると
\(9a^4-15a^2+8=0\)
\(a^2=s\) とおくと
\(9s^2-15s+8=0\)
この\(s\)の方程式の解は実数ではないので、\(a\)が実数にならないため不適。
以上から
\((a,b)=(±\displaystyle\frac{2\sqrt{6}}{9},∓\displaystyle\frac{2\sqrt{6}}{9})\) (複号同順)
(例題2)
曲線 \(y=x^3-x\) に3本の接線が引けるような 点\((a,b)\) の存在範囲を求めて、\(xy\)平面に図示せよ。
(解答)
曲線 \(y=x^3-x\) 上の点を\(P(t,t^3-t)\)とおく。
\(y’=3x^2-1\) より点\(P\)における接線の方程式は
\(y=(3t^2-1)(x-t)+t^3-t\)
整理して
\(y=(3t^2-1)x-2t^3\)
これが 点\((a,b)\)を通るから
\(b=(3t^2-1)a-2t^3\)
\(t\)について整理して
\(2t^3-3at^2+a+b=0\)・・・①
3次関数では接点が異なれば接線も異なるので、\(t\)の方程式①が3つの異なる実数解をもてば接線が3本存在することになる。
\(f(t)=2t^3-3at^2+a+b\) とおくと
\(f'(t)=6t(t-a)\)
\(f'(t)=0\) となるのは \(t=0,a\)
\(y=f(t)\)が\(x\)軸と異なる3点で交わればよいので、極値が存在し、極大値と極小値の値の積が負になればよい。
よって
\(a≠0\) かつ \(f(0)・f(a)<0\)
ゆえに
\(a≠0\) かつ \((a+b)(-a^3+a+b)<0\)
不等式は
\(a+b>0\) かつ \(-a^3+a+b<0\)
または
\(a+b<0\) かつ \(-a^3+a+b>0\)
すなわち
\(b>-a\) かつ \(b<a^3-a\)
または
\(b<-a\) かつ \(b>a^3-a\)
となるので領域を図示すると次の通り。
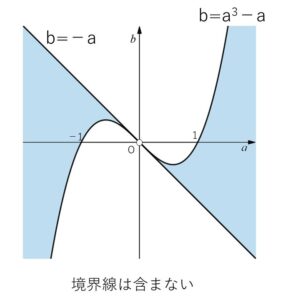
もう一方の \(b=-a\) は、変曲点(3次関数の点対称の中心)における接線です。この例題だと原点\((0,0)\)における接線です。
(参考)
接線が2本、1本引ける場合も同様に考えてまとめると次のような配置になります。
(原点以外の境界線が2本引ける場合になっています)
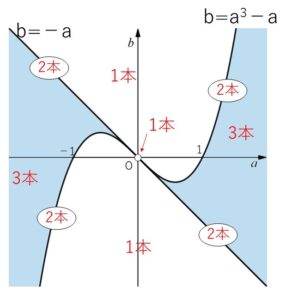
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→不等式と微分① back→接線の本数①