接線と法線の方程式について見ていきます。
内容は数ⅡBのときとほとんど同じです。
・接線の方程式
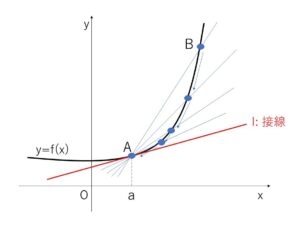
連続関数 \(y=f(x)\) において、曲線 \(y=f(x)\) 上に異なる2点\(A,B\) があるとき、点\(B\)を限りなく点\(A\)に近づけるとき、\(A,B\)を通る直線が限りなく近づく直線を\(l\)とします。
このとき、直線\(l\)を点\(A\)における接線、また点\(A\)を接点とよびます。
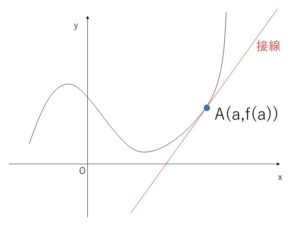
ここで曲線 \(y=f(x)\) が微分可能なとき、\(A(a,f(a))\) と \(B(a+h,f(a+h))\) を通る直線の傾き(平均変化率)は
\(\displaystyle\frac{f(a+h)-f(a)}{h}\)
であり、微分係数の定義から
\(f'(a)=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)
となるので、直線\(AB\)の傾きは限りなく\(f'(a)\)に近づきます。したがって、接線\(l\)の傾きは \(f'(a)\) であり、また接線\(l\)は 点\(A(a,f(a))\) を通ることから、その方程式は次のようになります。
\(y-f(a)=f'(a)(x-a)\)
なお「点\(A\)における接線」と「点\(A\)を通る接線」は違うものですが、詳しくは (1-3)ある点を通る接線 のところで扱いたいと思います。簡単にまとめると、「点\(A\)における接線」は接点が\(A\)である接線で、「点\(A\)を通る接線」は点\(A\)を通りさえすればよいので、ほかの点における接線がたまたま\(A\)を通る場合でも、接点が\(A\)であってもどちらもでよいです。
・法線の方程式
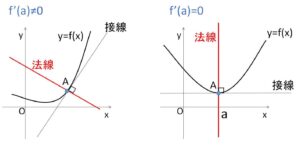
曲線 \(y=f(x)\) 上の 点\(A(a,f(a))\) を通り、点\(A\)における接線と垂直である直線を「点\(A\)における法線」といいます。
よって、\(f'(a)≠0\) のときの法線の傾きは \(-\displaystyle\frac{1}{f'(a)}\) となるので、その方程式は次の通りです。
\(y-f(a)=-\displaystyle\frac{1}{f'(a)}(x-a)\)
また、\(f'(a)=0\) のときは 法線は点\(A\)を通る\(y\)軸に平行な直線になるので、その方程式は
\(x=a\)
です。
(注)微分係数が存在しない場合の注意点
\(y=\sqrt[3]{x}\)・・・① の \(O(0,0)\) における接線について考えてみる。
\(y’=\displaystyle\frac{1}{3\sqrt[3]{x^2}}\)
となり、\(x=0\) における微分係数は存在しないので、接線がないように思える。
しかし、\(x\)を\(y\)の関数とみると①より
\(x=y^3\)・・・②
となり、②を(\(y\)で)微分すると
\(x’=3y^2\)
したがって、\(y=0\) における微分係数は \(x’=0\) となる。よって \(x=g(y)=y^3\) の \(y=0\) における接線と法線の方程式は
接線:\(x-0=0(y-0)\) つまり \(x=0\)・・・③
法線:\(y=0\)・・・④
となり、①②が同じ曲線を表すことから、接線は③、法線は④となる。
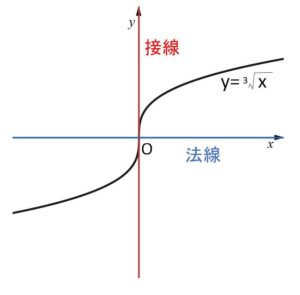
このような現象がおこるのは、この例のように微分係数が無限大に発散する場合です。接線が\(y\)軸に平行になるので、\(y=\cdots\) の形で接線を表すことができません。(接線は \(x=(定数)\) の形になる)
(例題)
\(a\)は正の定数とする。
曲線 \(y=f(x)=\displaystyle\frac{1}{2a}(e^{ax}+e^{-ax})\)
上の2点 \(P(t,f(t))\)、\(Q(-t,f(-t))\) をとり、\(P,Q\)における接線の交点を\(R\)、法線の交点を\(S\)とする。\(t\)を限りなく\(0\)に近づけたとき、次の点が次第に近づく点の座標をそれぞれ求めよ。
(1)\(R\) (2)\(S\)
グラフは必須ではないですが、書くと分かりやすくなると思います。(\(y\)軸対称になる)
(解答)
\(y=f(x)=\displaystyle\frac{1}{2a}(e^{ax}+e^{-ax})\)
\(f'(x)=\displaystyle\frac{1}{2a}(ae^{ax}-ae^{-ax})\)
\(=\displaystyle\frac{1}{2}(e^{ax}-e^{-ax})\)
(\(f'(x)=\displaystyle\frac{e^{2ax}-1}{2e^{ax}}\) より、
\(x>0\) のとき \(f'(x)>0\)、\(x<0\) のとき \(f'(x)<0\) からグラフが分かる)
(1)
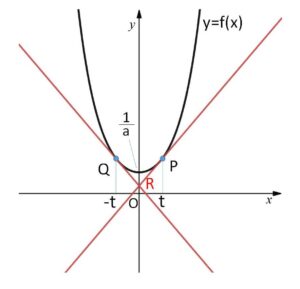
\(P\)における接線の方程式は
\(y-\displaystyle\frac{1}{2a}(e^{at}+e^{-at})=\displaystyle\frac{e^{at}-e^{-at}}{2}(x-t)\)・・・①
\(Q\)における接線の方程式は
\(y-\displaystyle\frac{1}{2a}(e^{at}+e^{-at})=-\displaystyle\frac{e^{at}-e^{-at}}{2}(x+t)\)・・・②
①-②より
\(0=\displaystyle\frac{e^{at}-e^{-at}}{2}(x-t)+\displaystyle\frac{e^{at}-e^{-at}}{2}(x+t)\)
\(t\)を限りなく\(0\)に近づけるので、\(t≠0\)。
ゆえに \(e^{at}-e^{-at}≠0\) だから
\(0=(x-t)+(x+t)\)
よって交点\(R\)の\(x\)座標は
\(x=0\) (グラフの対称性からも分かる)
①に\(x=0\)を代入して
\(y-\displaystyle\frac{1}{2a}(e^{at}+e^{-at})=\displaystyle\frac{e^{at}-e^{-at}}{2}\cdot(-t)\)
よって交点\(R\)の\(y\)座標は
\(y=\displaystyle\frac{1}{2a}(e^{at}+e^{-at})-\displaystyle\frac{t(e^{at}-e^{-at})}{2}\)
\(R(0,\displaystyle\frac{1}{2a}(e^{at}+e^{-at})-\displaystyle\frac{t(e^{at}-e^{-at})}{2})\)
したがって \(t \to 0\) のとき
\(R \to (0,\displaystyle\frac{1+1}{2a}-\displaystyle\frac{0\cdot(1-1)}{2})\)
\(R\)の近づく点の座標は
\((0,\displaystyle\frac{1}{a})\)
(2)
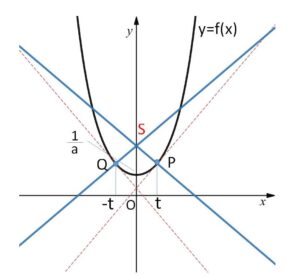
\(P\)における法線の方程式は
\(y-\displaystyle\frac{1}{2a}(e^{at}+e^{-at})=-\displaystyle\frac{2}{e^{at}-e^{-at}}(x-t)\)・・・③
\(Q\)における法線の方程式は
\(y-\displaystyle\frac{1}{2a}(e^{at}+e^{-at})=\displaystyle\frac{2}{e^{at}-e^{-at}}(x+t)\)・・・④
④-③より
\(0=\displaystyle\frac{2}{e^{at}-e^{-at}}(x+t)+\displaystyle\frac{2}{e^{at}-e^{-at}}(x-t)\)
よって交点\(S\)の\(x\)座標は
\(x=0\) (これも対称性から分かる)
①に\(x=0\)を代入して整理すると、\(S\)の\(y\)座標は
\(y=\displaystyle\frac{1}{2a}(e^{at}+e^{-at})+\displaystyle\frac{2t}{e^{at}-e^{-at}}\)
\(S(0,\displaystyle\frac{1}{2a}(e^{at}+e^{-at})+\displaystyle\frac{2t}{e^{at}-e^{-at}})\)
微分の定義を利用するか、\(\displaystyle\lim_{t \to 0}\displaystyle\frac{e^t-1}{t}=1\) を利用します。
ここで
\(\displaystyle\lim_{t \to 0}\displaystyle\frac{2t}{e^{at}-e^{-at}}\)
\(=\displaystyle\lim_{t \to 0}\displaystyle\frac{2}{\displaystyle\frac{e^{at}-e^{-at}}{t}}\)
\(=\displaystyle\lim_{t \to 0}\displaystyle\frac{2}{\displaystyle\frac{e^{at}-1+1-e^{-at}}{t}}\)
\(=\displaystyle\lim_{t \to 0}\displaystyle\frac{2}{\displaystyle\frac{e^{at}-1}{at}\cdot a+\displaystyle\frac{e^{-at}-1}{-at}\cdot a}\)
\(=\displaystyle\frac{2}{a+a}\)
\(=\displaystyle\frac{1}{a}\)
したがって\(S\)は
\((0,\displaystyle\frac{1}{a}+\displaystyle\frac{1}{a})=\)\((0,\displaystyle\frac{2}{a})\)
に近づく。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→陰関数・媒介変数表示と接線