共通接線(接点が異なる場合)の例題です。
①接点の\(x\)座標をそれぞれ、文字\(s,t\)でおいて、接線が一致すると考える
②一方の接線が、もう一方の曲線に接すると考える
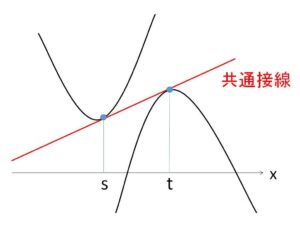
しかし、数Ⅲの範囲では重解条件などが使えない場合が多いので、基本的には①の解法手段をとります。なお、2曲線が接する(共有点をもち、その共有点の接線が一致する)場合は、これらの特殊例になります。(\(s=t\)の場合)
(例題)
2つの曲線
\(y=-e^{-x}\)・・・①
\(y=e^{ax}\) (\(a>0\)) ・・・②
のどちらにも接する直線を\(l\)とする。\(l\)と①の接点 および \(l\)と②の接点 の\(x\)座標をそれぞれ求めよ。
(解答)
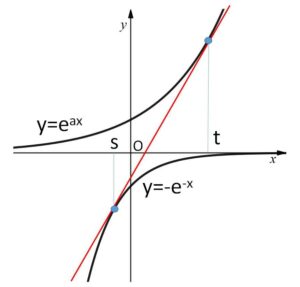
\(y=-e^{-x}\)・・・①
\(y=e^{ax}\) (\(a>0\)) ・・・②
①での接点を \((s,-e^{-s})\)、②での接点を \((t,e^{at})\) とおく。
①②を微分するとそれぞれ
\(y’=e^{-x}\)・・・①’
\(y’=ae^{ax}\)・・・②’
となるので、接線の方程式は次の2通りに表すことができる。
\(y=e^{-s}(x-s)-e^{-s}\)・・・③
\(y=ae^{at}(x-t)+e^{at}\)・・・④
③④が一致するので、傾きと\(y\)切片が等しいから
\(e^{-s}=ae^{at}\)・・・⑤
\(-(s+1)e^{-s}=(-at+1)e^{at}\)・・・⑥
以下 \(a>0\) に注意する。⑤で自然対数をとると
\(-s=\log a+at\)
\(at=-s-\log a\)・・・⑦
⑦を⑥に代入して
\(-(s+1)e^{-s}=(s+\log a+1)\cdot\displaystyle\frac{e^{-s}}{a}\)
もしくは、⑤から \(e^{at}=\displaystyle\frac{e^{-s}}{a}\) としてもよいです。
\(e^{-s}\ (>0)\) で割って、\(a\)倍すると
\(-a(s+1)=(s+\log a+1)\)
よって
\((a+1)s=-\log a-a-1\)
\(s=-\displaystyle\frac{\log a}{a+1}-1\) (①の接点の\(x\)座標)
また⑦より
\(at=\displaystyle\frac{\log a}{a+1}+1-\log a\)
\(at=-\displaystyle\frac{a\log a}{a+1}+1\)
ゆえに
\(t=-\displaystyle\frac{\log a}{a+1}+\displaystyle\frac{1}{a}\) (②の接点の\(x\)座標)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接する2曲線 back→ある点を通る接線