ある点を通る接線

点\(A\)における接線と、点\(A\)を通る接線の違いについて見ていきます。

・点\(A\)を通る接線と点\(A\)における接線
「点\(A\)における接線」は、点\(A\)が接点となる接線です。これに対して、「点\(A\)を通る接線」は接線が点\(A\)を通りさえすればよいので、

(ア)他の点における接線がたまたま点\(A\)を通る場合
(イ)点\(A\)における接線となる場合

が考えらえれます。

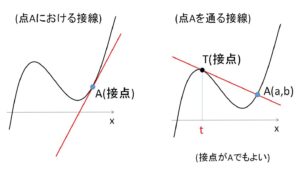
なお、「点\(A\)を通る接線」関連の問題は、接点の\(x\)座標を未知数\(t\)とおくことで接線の方程式を立てて(\(t\)とおくことで、微分から接線の方程式が簡単に分かる)、点\((a,b)\)を通ることからこの方程式に\(a,b\)を代入するという解き方をするのが定石です。

(例題)
\(f(x)=\displaystyle\frac{\log x}{x}\) とするとき、\(y=f(x)\) の接線のうち原点を通るものを求めよ。

(解答)
接点を \((t,\displaystyle\frac{\log t}{t})\)  (\(t>0\)) とおく。

\(f'(x)=\displaystyle\frac{\displaystyle\frac{1}{x}\cdot x-\log x\cdot1}{x^2}\)

\(=\displaystyle\frac{1-\log x}{x^2}\)

だから、接線の方程式は
\(y-\displaystyle\frac{\log t}{t}=\displaystyle\frac{1-\log t}{t^2}(x-t)\)・・・①

接線は原点を通るので、①に \(x=0\)、\(y=0\) を代入して
\(-\displaystyle\frac{\log t}{t}=\displaystyle\frac{1-\log t}{t^2}\cdot(-t)\)

\(-t\)倍して整理すると
\(2\log t=1\)
\(\log t=\displaystyle\frac{1}{2}\)

よって
\(t=e^{\frac{1}{2}}\)・・・②

したがって接線の方程式は①に②を代入して
\(y-\displaystyle\frac{\displaystyle\frac{1}{2}}{e^{\frac{1}{2}}}=\displaystyle\frac{1-\displaystyle\frac{1}{2}}{e}(x-e^{\frac{1}{2}})\)

整理すると
\(y=\displaystyle\frac{1}{2e}x\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2曲線に接する直線　back→陰関数・媒介変数表示と接線