2曲線が接する問題について見ていきます。
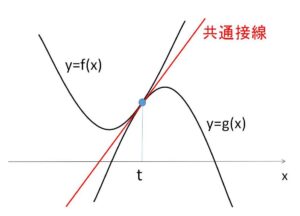
「2曲線が接する」とは、2曲線が共有点をもち、その共有点での接線が一致することをいいます。共有点の\(x\)座標を\(t\)とすると、\(y=f(x)\) と \(y=g(x)\) が接する条件は次の2式で表されます。
\(f(t)=g(t)\)・・・① (共有点について)
\(f'(t)=g'(t)\)・・・② (接線の傾きについて)
(接線の\(y\)切片が一致する条件については、①により保証されているので、必要ありません)
(例題)
\(y=e^{2x}\) と \(y=a\sqrt{x}\) (\(x>0\)) が共有点をもち、その点における2曲線の接線が一致するような定数\(a\)を定めよ。
(解答)
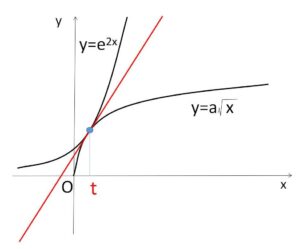
共有点の\(x\)座標を\(t\)とおく。(\(t>0\))
\(y=e^{2x}\)・・・①
\(y=a\sqrt{x}\)・・・②
においてそれぞれ微分すると
\(y’=2e^{2x}\)
\(y=\displaystyle\frac{a}{2\sqrt{x}}\)
よって、共有点において接線が一致するためには
\(e^{2t}=a\sqrt{t}\)・・・③
\(2e^{2t}=\displaystyle\frac{a}{2\sqrt{t}}\)・・・④
(あとは連立方程式③④から \(a\ (t)\) を求めるだけです。)
③より \(a=\displaystyle\frac{e^{2t}}{\sqrt{t}}\)・・・⑤
これを④に代入して
\(2e^{2t}=\displaystyle\frac{e^{2t}}{2t}\)
\(e^{2t}≠0\) より、両辺これで割って
\(2=\displaystyle\frac{1}{2t}\) だから \(t=\displaystyle\frac{1}{4}\ (>0)\)
したがって⑤より
\(a=\displaystyle\frac{e^{\frac{1}{2}}}{\displaystyle\frac{1}{2}}\)\(=2\sqrt{e}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→共有点での接線のなす角 back→2曲線に接する直線