平均値の定理とガウス記号の融合問題です。
(例題1)
\(x>0\) とし、\(f(x)=\log x^{100}\) とおく。
(1)次の不等式を証明せよ。
\(\displaystyle\frac{100}{x+1}<f(x+1)-f(x)<\displaystyle\frac{100}{x}\)
(2)実数\(a\)の整数部分 (\(k≦a<k+1\) となる整数\(k\)) を\([a]\)で表す。整数\([f(1)],[f(2)],[f(3)],\cdots,[f(1000)]\) のうちで異なるものの個数を求めよ。必要ならば \(\log10=2.3026\) として計算せよ。
(解答)
(1)
示したい不等式は
\(\displaystyle\frac{100}{x+1}<\log(x+1)^{100}-\log x^{100}<\displaystyle\frac{100}{x}\)
なので
\(\displaystyle\frac{1}{x+1}<\log(x+1)-\log x<\displaystyle\frac{1}{x}\)
を証明すればよい。
\(f(x)=\log x\) は、\(x>0\)で微分可能(連続でもある)なので、平均値の定理より
\(\displaystyle\frac{\log(x+1)-\log x}{(x+1)-x}=\displaystyle\frac{1}{c}\)・・・①
\(x<c<x+1\)・・・②
を満たす\(c\)が存在する。②より
\(\displaystyle\frac{1}{x+1}<\displaystyle\frac{1}{c}<\displaystyle\frac{1}{x}\)
となるので、これと①より
\(\displaystyle\frac{1}{x+1}<\log(x+1)-\log x<\displaystyle\frac{1}{x}\)
(2)
\(50<f(2)-f(1)<100\)
\(\displaystyle\frac{100}{3}<f(3)-f(2)<50\)
\(25<f(4)-f(3)<\displaystyle\frac{100}{3}\)
としばらくは隣との差が\(1\)以上になるので、整数部分は異なるものになりますが、\(1\)より小さくなると「整数部分が異なる場合と同じになる場合」が考えられます。
(1)より
\(\displaystyle\frac{100}{x+1}<f(x+1)-f(x)<\displaystyle\frac{100}{x}\)
(ア)
\(\displaystyle\frac{100}{x+1}=1\) を解くと \(x=99\) だから
\(1≦x≦99\) のとき
\(1<f(x+1)-f(x)\) より
\([f(1)],[f(2)],[f(3)]\cdots,[f(99)],[f(100)]\) はすべて異なる整数になる。
(イ)
\(100≦x\) のとき
\(f(x+1)-f(x)<1\)
あとは実際にどの自然数の間をとるかを計算する、つまり\([f(100)]\)と\([f(1000)]\)を計算するだけです。
よって
\([f(x+1)]=[f(x)]\) または \([f(x+1)]=[f(x)]+1\)
となるので、\([f(x)]\) の値は \([f(100)]\) から \([f(1000)]\) までの値をくまなくとる。
ここで
\([f(100)]=[\log 100^{100}]=[200\log10]\)
\(=[200×2.3026]=[460.52]=\color{blue}{460}\)
\([f(1000)]=[\log 1000^{100}]=[300\log10]\)
\(=[300×2.3026]=[690.78]=\color{blue}{690}\)
ゆえに
\([f(100)],[f(101)],\cdots,[f(1000)]\) のうち異なるものの個数は
\(690-460+1=231\)
(ア)(イ)より、\([f(100)]\) の重複に注意して求める個数は
\(99+231=\)\(330\)
(例題2)
実数\(a\)に対して \(k≦a<k+1\) をみたす整数\(k\)を\([a]\)で表す。\(n\)を正の整数として
\(f(x)=\displaystyle\frac{x^2(2\cdot3^3\cdot n-x)}{2^5\cdot3^3\cdot n^2}\)
とおく。\(36n+1\) 個の整数
\([f(0)],[f(1)],[f(2)],\cdots,[f(36n)]\)
のうち相異なるものの個数を\(n\)を用いて表せ。
(解答)
\(0≦x≦36n\) の範囲で考える。
\(f(x)=\displaystyle\frac{x^2(2\cdot3^3\cdot n-x)}{2^5\cdot3^3\cdot n^2}\)
\(f'(x)=\displaystyle\frac{(2\cdot3^3\cdot n\cdot2x-3x^2)}{2^5\cdot3^3\cdot n^2}=\displaystyle\frac{x(36n-x)}{2^5\cdot3^2\cdot n^2}\)
よって \(y=f(x)\) のグラフは次の通り。(\(0≦x≦36n\) で単調増加)
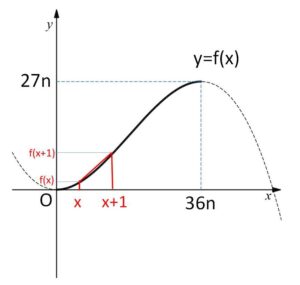
ここで平均値の定理より
\(\displaystyle\frac{f(x+1)-f(x)}{(x+1)-1}=f'(c)\)、\(x<c<x+1\)
つまり
\(f(x+1)-f(x)=f'(c)\)・・・①
\(x<c<x+1\)・・・②
を満たす\(c\)が存在する。
また
\(f'(x)=1\) を解くと
\(\displaystyle\frac{x(36n-x)}{2^5\cdot3^2\cdot n^2}=1\) より
\(x^2-36nx+2^5\cdot3^2\cdot n^2=0\)
\((x-12n)(x-24n)=0\)
\(x=12n,24n\)
よって、\(f'(x)=\displaystyle\frac{x(36n-x)}{2^5\cdot3^2\cdot n^2}\) (2次関数)
のグラフは次の通り。
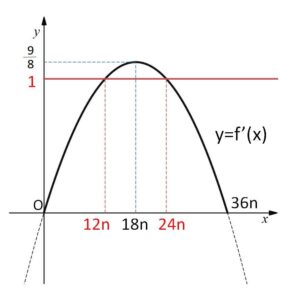
ゆえに
\(0<x<12n\) のとき \(0<f'(x)<1\)
\(12n<x<24n\) のとき \(f'(x)>1\)
\(24n<x<36n\) のとき \(0<f'(x)<1\)
したがって、\(x<c<x+1\)・・・②
\(f(x+1)-f(x)=f'(c)\)・・・①より
(\(x\)が整数のとき \(c\) は整数にならない)
(ア)\(x=0,1,2,\cdots,12n-1\) のとき
\(0<f(x+1)-f(x)<1\)
(イ)\(x=12n,12n+1,\cdots,24n-1\) のとき
\(f(x+1)-f(x)>1\)
(ウ)\(x=24n,24n+1,\cdots,36n-1\) のとき
\(0<f(x+1)-f(x)<1\)
(ア)より \([f(0)],[f(1)]\cdots,[f(12n)]\) が、\([f(0)]\) から \([f(12n)]\) までの整数をくまなくとるので
\([f(0)]=0\)
\([f(12n)]=7n\) より
\([f(0)],[f(1)]\cdots,[f(12n)]\) のうち相異なるものの個数は \(7n+1\) 個
(イ)より、\([f(12n)],[f(12n+1)],\cdots,[f(24n)]\) はすべて異なる整数となるから、これらのうち相異なるものの個数は \(12n+1\) 個
(ウ)より(ア)と同様に \([f(24n)],[f(24n+1)]\cdots,[f(36n)]\)が、\([f(24n)]\) から \([f(36n)]\) までの整数をくまなくとるので
\([f(24n)]=20n\)
\([f(36n)]=27n\) より
\([f(24n)],[f(24n+1)]\cdots,[f(36n)]\) のうち相異なるものの個数は \(7n+1\) 個
以上より \([f(12n)],[f(24n)]\) の重複に注意すると、求める個数は
\((7n+1)+(12n+1)+(7n+1)-2\)
\(=26n+1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→第1次導関数と関数の増減 back→平均値の定理と漸化式