導関数 \(f'(x)\) の符号と関数の増減の関係について見ていきます。
丁寧に示すなら、平均値の定理を用いることになります。
・\(f'(x)\)の符号と関数の増減
関数\(f(x)\)が、閉区間\([a,b]\)で連続で、開区間\((a,b)\)で微分可能なとき、関数の増減について次のことが成り立ちます。
開区間\((a,b)\)で常に
(i)\(f'(x)>0\) のとき \(f(x)\) は閉区間\([a,b]\)で単調に増加する。
(ii)\(f'(x)<0\) のとき \(f(x)\) は閉区間\([a,b]\)で単調に減少する。
(iii)\(f'(x)=0\) のとき \(f(x)\) は閉区間\([a,b]\)で定数である。(一定である)
「閉区間\([a,b]\)で連続で、開区間\((a,b)\)で微分可能」という条件より平均値の定理が利用できます。
(証明)
(i)について
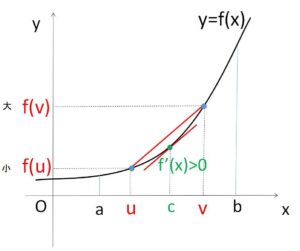
区間\([a,b]\)で、\(a≦u<v≦b\) となる任意の\(u,v\)をとる。
平均値の定理から
\(f(v)-f(u)=f'(c)(v-u)\)・・・①
\(u<c<v\)
を満たす、\(c\)が存在する。条件より \(f'(c)>0\)。\(v-u>0\) と合わせて①より
\(f(v)-f(u)>0\)
つまり
\(f(v)>f(u)\) (単調増加)
(ii)(iii)も同様に平均値の定理から示すことができる。
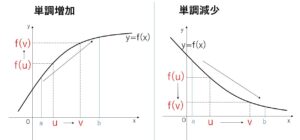
(補足1)単調増加(単調減少)の定義
関数\(f(x)\)について、ある区間内の任意の\(u,v\)について
\(u<v\) ならば \(f(u)<f(v)\) が成り立つとき
\(f(x)\)はその区間で単調増加であるといい
\(u<v\) ならば \(f(u)>f(v)\) が成り立つとき
\(f(x)\)はその区間で単調減少であるといいます。
単調増加のときはグラフが右上がり、単調減少のときは右下がりです。
なお上の例では、区間が 閉区間 \(a≦x≦b\) で、この閉区間で\(f(x)\)が単調増加(単調減少)ということになっています。
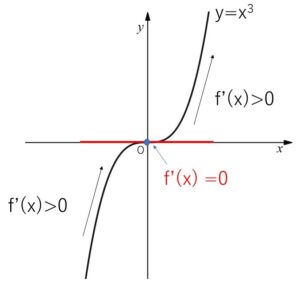
(補足2)\(f'(x)≧0\) や \(f'(x)≦0\) の扱い
\(f'(x)≧0\) の場合も、\(f'(x)=0\) となる\(x\)が点在しているに過ぎない場合は、単調増加になります。(\(f'(x)≦0\) のときも同様)
例えば、\(f(x)=x^3\) では、\(f'(x)=3x^2\) より
\(x=0\) のときのみ \(f'(x)=0\)、\(x≠0\) のときは \(f'(x)>0\) となりますが、実数全体の\(x\)で単調増加する関数です。
これは、\(x≦0\) と \(x≧0\) で分けて考えることで
\(x≦0\) で連続、\(x<0\) で微分可能で\(f'(x)>0\)だから、\(x≦0\) で単調増加、
\(x≧0\) でも同様に単調増加になるので、全体としても単調増加になることが分かります。
(補足3)端点について
連続性の条件を閉区間\([a,b]\)でなく、開区間\((a,b)\)にすると単調増加とならないことがあります。下図では、\(a≦x≦b\) では単調増加にはなっていません。(\(a<x≦b\) では単調増加になっている) また、証明に使った平均値の定理も利用できません。
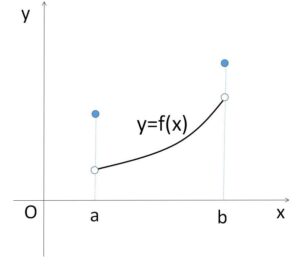
なお微分可能性に関しては、端点を含んでいても構いません。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極値 back→グラフの増加率とガウス記号