極値について見ていきます。
・極値
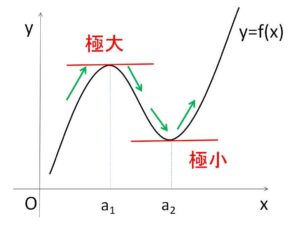
関数\(f(x)\)は連続関数であるとします。
\(x=a\) を含む十分小さい開区間・・・(注)において、\(x≠a\) ならば \(f(a)>f(x)\) を満たすとき、\(f(x)\)は \(x=a\) で極大であるといい、\(f(a)\) を極大値といいます。
同様に、\(x=a\) を含む十分小さい開区間において、\(x≠a\) ならば \(f(a)<f(x)\) を満たすとき、\(f(x)\)は \(x=a\) で極小であるといい、\(f(a)\) を極小値といいます。
また、極大値と極小値をまとめて極値とよびます。
(つまり小さな1部分を考えて、最大値や最小値をとる場合が、極大・極小になるということ)
(注)
開区間を考えるのは、閉区間だと端点で最大値(最小値)をとる場合があるからです。この場合を極値としてしまうのを避けるために開区間にしています。
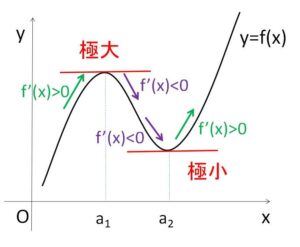
極値をとる前後のグラフの増減を調べると、
極大値:増加→減少
極小値:減少→増加
となっているので、\(f(x)\)が \(x=a\) 付近で微分可能であるとき
「\(x<a\) で \(f'(x)>0\)、\(x>a\) で \(f'(x)<0\)」 ならば \(f(a)\) は極大値
「\(x<a\) で \(f'(x)<0\)、\(x>a\) で \(f'(x)>0\)」 ならば \(f(a)\) は極小値
となります。つまり\(f'(x)\)の符号が入れかわるときに極値をとり、正から負に変わるときは極大、負から正に変わるときは極小になります。
したがって\(x=a\)で極値をとる場合の \(x=a\) における微分係数は、\(f'(a)=0\) となりそうですが、実際次の定理が成り立ちます。
関数\(f(x)\)が\(x=a\)で微分可能であるとする。このとき
「\(f(x)\)が\(x=a\)で極値をとるならば、\(f'(a)=0\)」
(逆は成り立たない)
グラフから視覚的に \(f'(a)=0\) となることは分かりますが、証明は次の通りです。
(証明)
まず \(x=a\) で極大値をとるときを考える。
十分小さい\(|Δx|\)について
\(f(a)>f(a+Δx)\) が成り立つので
\(f(a+Δx)-f(a)<0\)・・・①
\(Δx>0\) のとき①より
\(\displaystyle\frac{f(a+Δx)-f(a)}{Δx}<0\)
よって、\(Δx \to +0\) とすると
\(\displaystyle\lim_{Δx \to +0}\displaystyle\frac{f(a+Δx)-f(a)}{Δx}≦0\) (極限をとると=がつく)
同様に\(Δx<0\) のとき①より
\(\displaystyle\lim_{Δx \to -0}\displaystyle\frac{f(a+Δx)-f(a)}{Δx}≧0\)
\(x=a\) で微分可能だから、極限値が存在し(両側極限が一致し)
\(\displaystyle\lim_{Δx \to 0}\displaystyle\frac{f(a+Δx)-f(a)}{Δx}=f'(a)=0\)
\(x=a\) で極小値をとるときも同じように \(f'(a)=0\) となる。
まず逆が成り立たないこと、それと微分可能でない場合でも極値をとる場合があることです。
ただしこの定理の逆は成り立ちません。つまり \(f'(a)=0\) となる場合でもその前後で\(f'(x)\)の符号が入れかわらない場合には極値をとりません。
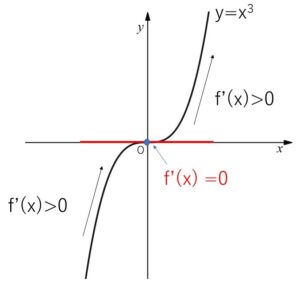
(例)\(f(x)=x^3\)
\(f'(x)=3x^2\)
\(f'(x)=0\) となるのは \(x=0\) だが、
\(x<0\) で \(f'(x)>0\)、\(x>0\) で \(f'(x)>0\) となり(符号が変わらない)、実数全体の\(x\)で単調増加。
よって\(x=0\)で極値をとらない。
また、\(f(x)\)が\(x=a\)で微分可能でない場合でも極値をとる場合もあります。
(例)\(f(x)=|x|\)
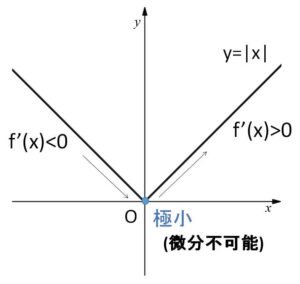
\(x=0\) で微分不可能だが
\(x<0\) のとき \(f'(x)=-1\ (<0)\)、\(x>0\) のとき \(f'(x)=1\ (>0)\)
となるので、
\(x≦0\) で単調減少、\(x≧0\) で単調増加。
よって、\(x=0\) で極小値をとる。
いずれにせよ、極値やグラフの増減を整理するには増減表を作ることが有効になります。
(例題)
\(f(x)=\sin^3x+\cos^3x\) (\(0≦x≦π\))
について、\(f(x)\)の極小値、極大値とそのときの\(x\)の値を求めよ。
(解答)
\(f'(x)=3\sin^2x\cos x+3\cos^2x(-\sin x)\)
\(=3\sin x\cos x(\sin x-\cos x)\)
(合成して差の部分をまとめると)
\(=3\sin x\cos x\cdot\sqrt{2}\sin(x-\displaystyle\frac{π}{4})\)
よって増減表は次の通りになるから
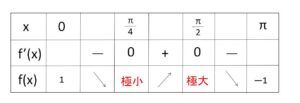
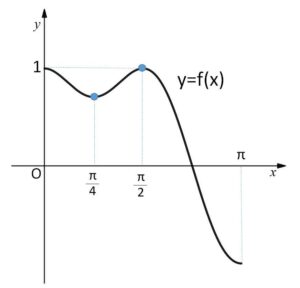
極大値 \(x=\displaystyle\frac{π}{2}\) のとき \(f(\displaystyle\frac{π}{2})=1\)
極小値 \(x=\displaystyle\frac{π}{4}\) のとき \(f(\displaystyle\frac{π}{4})=\displaystyle\frac{1}{\sqrt{2}}\)
(参考) \(y=f(x)=\sin^3x+\cos^3x\) のグラフ
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極値をもつ条件 back→第1次導関数と関数の増減