極値をもつ条件に関する例題です。
ポイントは導関数の符号の変化です。
(例題)
\(k\)を正の定数とする。関数
\(f(x)=\displaystyle\frac{1}{x}-\displaystyle\frac{k}{(x+1)^2}\) (\(x>0\))
\(g(x)=\displaystyle\frac{(x+1)^3}{x^2}\) (\(x>0\))
について
(1)\(\displaystyle\lim_{x \to +0}g(x)\)、\(\displaystyle\lim_{x \to \infty}g(x)\) をそれぞれ求めよ。
(2)\(g(x)\)の増減を調べよ。
(3)\(f(x)\)が極値をもつような定数\(k\)の値の範囲を求めよ。
(4)\(f(x)\)が\(x=a\)で極値をとるとき、極値\(f(a)\)を\(a\)だけの式で表せ。
(5)\(k\)が(3)で求めた範囲にあるとき、\(f(x)\)の極大値は\(\displaystyle\frac{1}{8}\)より小さいことを示せ。
(1)
\(\displaystyle\lim_{x \to +0}\displaystyle\frac{(x+1)^3}{x^2}=+\infty\) (\(\displaystyle\frac{1}{+0}\) より)
\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{(x+1)^3}{x^2}\)\(=\displaystyle\lim_{x \to \infty}(x+3+\displaystyle\frac{3}{x}+\displaystyle\frac{1}{x^2})\)\(=+\infty\)
(2)
\(g(x)=\displaystyle\frac{(x+1)^3}{x^2}\) (\(x>0\))
を微分して
\(g'(x)=\displaystyle\frac{3(x+1)^2\cdot x^2-(x+1)^3\cdot2x}{x^4}\)
\(=\displaystyle\frac{(x+1)^2(x-2)}{x^3}\)
よって増減表は次の通り。
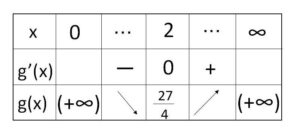
(3)
\(f'(x)\)をうまく変形すると、\(g(x)\)が出てきます。
\(f(x)=\displaystyle\frac{1}{x}-\displaystyle\frac{k}{(x+1)^2}\) (\(x>0\))
微分して
\(f'(x)=-\displaystyle\frac{1}{x^2}+\displaystyle\frac{2k}{(x+1)^3}\)
\(=\displaystyle\frac{1}{(x+1)^3}\cdot\left\{2k-\displaystyle\frac{(x+1)^3}{x^2}\right\}\)
\(=\displaystyle\frac{1}{(x+1)^3}\cdot\{2k-g(x)\}\)
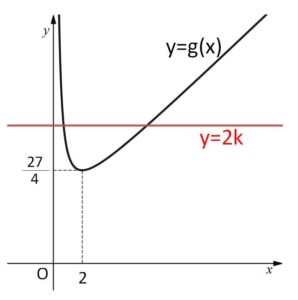
\(f(x)\)が極値をもつためには、\(f'(x)\)の符号の変化があればよい。
\(y=2k\)、\(y=g(x)\) のグラフより、これらが異なる2点で交わればよいので
\(2k>\displaystyle\frac{27}{4}\)
したがって
\(k>\displaystyle\frac{27}{8}\)
(4)
つまり、\(2k-g(a)=0\) であり、この式から\(k\)を消去できます。
\(f'(a)=0\) だから(3)より
\(2k-g(a)=0\)
つまり
\(k=\displaystyle\frac{(a+1)^3}{2a^2}\)
よって
\(f(a)=\displaystyle\frac{1}{a}-\displaystyle\frac{k}{(a+1)^2}\)
\(=\displaystyle\frac{1}{a}-\displaystyle\frac{1}{(a+1)^2}\cdot\displaystyle\frac{(a+1)^3}{2a^2}\)
\(=\displaystyle\frac{a-1}{2a^2}\)
(5)
また、\(β\)はどんな値でもよいわけではなく、グラフより\(β>2\)という制限がつきます。あとはこの制限のもとで(4)で求めた式のとりうる値を考えるだけです。
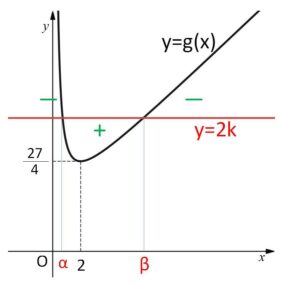
グラフの2交点の\(x\)座標を \(x=α,β\) (\(α<β\)) とおく。
\(2k-g(x)\) の符号が正から負に変わる境目は \(x=β\) のときで、このとき極大値\(f(β)\)をとる。
また、\(k>\displaystyle\frac{27}{8}\) のとき、グラフより \(β>2\)。
(4)より
\(f(β)=\displaystyle\frac{β-1}{2β^2}\)
\(=\displaystyle\frac{1}{2}\left\{-\displaystyle\frac{1}{β^2}+\displaystyle\frac{1}{β}\right\}\)
\(=\displaystyle\frac{1}{2}\left\{-(\displaystyle\frac{1}{β}-\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{4}\right\}\)
\(=-\displaystyle\frac{1}{2}(\displaystyle\frac{1}{β}-\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{8}\)
\(β>2\) より \(0<\displaystyle\frac{1}{β}<\displaystyle\frac{1}{2}\) だから
\(f(β)<\displaystyle\frac{1}{8}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極値と条件 back→極値