最大値・最小値に関する例題です。
微分して増減を考えていきます。
(例題)
実数\(a\) (\(0<a≦\displaystyle\frac{π}{3}\)) に対し、
\(f(x)=3\sin(\displaystyle\frac{x}{3})+\sin(a-x)\) (\(0≦x≦π\))
とする。
(1)\(4\sin\displaystyle\frac{π}{12}\) の値を求めよ。また、\(4\sin\displaystyle\frac{π}{12}\) と \(\sqrt{3}\) のどちらが大きいかを判定せよ。
(2)\(f'(x)=0\) となる\(x\) (\(0<x<π\)) を求めよ。
(3)\(f(x)\) (\(0≦x≦π\)) の最大値\(M(a)\)と最小値\(m(a)\)を求めよ。
(4)\(M(a)\)と\(m(a)\) (\(0<a≦\displaystyle\frac{π}{3}\)) のそれぞれについて取り得る値の範囲を求めよ。
(解答)
(1)
\(\sin\displaystyle\frac{π}{12}\)
\(=\sin(\displaystyle\frac{π}{4}-\displaystyle\frac{π}{6})\)
\(=\displaystyle\frac{1}{\sqrt{2}}\cdot\displaystyle\frac{\sqrt{3}}{2}-\displaystyle\frac{1}{\sqrt{2}}\cdot\displaystyle\frac{1}{2}\)
\(=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}\)
よって
\(4\sin\displaystyle\frac{π}{12}=\sqrt{6}-\sqrt{2}\)
(\(\sqrt{6}-\sqrt{2}≒2.4-1.4=1.0\) なので、\(\sqrt{3}\) のほうが大きいと予想できます)
また
\((\sqrt{3})^2-(\sqrt{6}-\sqrt{2})^2\)
\(=3-(8-4\sqrt{3})\)
\(=4\sqrt{3}-5\)
\(>4\cdot1.7-5>0\)
よって
\(\sqrt{3}>4\sin\displaystyle\frac{π}{12}\)
(2)
\(f(x)=3\sin(\displaystyle\frac{x}{3})+\sin(a-x)\)
\(f'(x)=\cos(\displaystyle\frac{x}{3})-\cos(a-x)\)
(和積でまとめます)
\(=-2\sin\left(\displaystyle\frac{a-\displaystyle\frac{2}{3}x}{2}\right)\sin\left(\displaystyle\frac{\displaystyle\frac{4}{3}x-a}{2}\right)\)
\(=-2\sin\left(\displaystyle\frac{a}{2}-\displaystyle\frac{x}{3}\right)\sin\left(\displaystyle\frac{2x}{3}-\displaystyle\frac{a}{2}\right)\)
(\(\sin\)の中身の範囲を絞ります)
\(0<a≦\displaystyle\frac{π}{3}\)、\(0<x<π\) より
\(-\displaystyle\frac{π}{3}<\displaystyle\frac{a}{2}-\displaystyle\frac{x}{3}<\displaystyle\frac{π}{6}\)、 \(-\displaystyle\frac{π}{6}<\displaystyle\frac{2x}{3}-\displaystyle\frac{a}{2}<\displaystyle\frac{2π}{3}\)
となるから、\(f'(x)=0\) を満たすのは
\(\displaystyle\frac{a}{2}-\displaystyle\frac{x}{3}=0\) または \(\displaystyle\frac{2x}{3}-\displaystyle\frac{a}{2}=0\)
よって
\(x=\displaystyle\frac{3}{2}a,\displaystyle\frac{3}{4}a\)
(3)
\(f'(x)=2\sin\left(\displaystyle\frac{x}{3}-\displaystyle\frac{a}{2}\right)\sin\left(\displaystyle\frac{2x}{3}-\displaystyle\frac{a}{2}\right)\)
と、(2)の結果より増減表は次の通り。
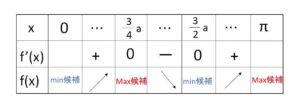
\(f(x)=3\sin(\displaystyle\frac{x}{3})+\sin(a-x)\)
まず最大値について
\(f(\displaystyle\frac{3}{4}a)\) または \(f(π)\) が候補。
\(f(\displaystyle\frac{3}{4}a)=4\sin\displaystyle\frac{1}{4}a\)
\(f(π)=\displaystyle\frac{3\sqrt{3}}{2}-\sin a\)
(大小比較のために差をとって微分していきます)
\(f(π)-f(\displaystyle\frac{3}{4}a)\)
\(=\displaystyle\frac{3\sqrt{3}}{2}-\sin a-4\sin\displaystyle\frac{1}{4}a\)
(\(=g(a)\)とおく)
\(g'(a)=-\cos a-\cos\displaystyle\frac{1}{4}a<0\) (∵ \(0<a≦\displaystyle\frac{π}{3}\))
したがって\(g(a)\)は単調減少関数なので
\(g(a)≧g(\displaystyle\frac{π}{3})=\sqrt{3}-4\sin\displaystyle\frac{π}{12}>0\) ((1)より)
ゆえに
\(g(a)>0\) となるから
最大値は\(f(π)\)となり
\(M(a)=\displaystyle\frac{3\sqrt{3}}{2}-\sin a\)
次に最小値については
\(f(0)\) または \(f(\displaystyle\frac{3}{2}a)\) が候補。
\(f(0)=\sin a\)
\(f(\displaystyle\frac{3}{2}a)=2\sin\displaystyle\frac{a}{2}\)
(こちらも差をとって微分でもよいが次のように変形すると楽)
ここで \(0<a≦\displaystyle\frac{π}{3}\) より
\(f(0)=2\sin\displaystyle\frac{a}{2}\cos\displaystyle\frac{a}{2}<2\sin\displaystyle\frac{a}{2}\)
となるから
\(f(0)<f(\displaystyle\frac{3}{2}a)\)
ゆえに最小値は\(f(0)\)で
\(m(a)=\sin a\)
(4)
不等号の=に気をつけるくらいです。
\(M(a)=\displaystyle\frac{3\sqrt{3}}{2}-\sin a\)
\(m(a)=\sin a\)
\(0<a≦\displaystyle\frac{π}{3}\) においてとりうる値の範囲は
\(\sqrt{3}≦M(a)<\displaystyle\frac{3\sqrt{3}}{2}\)
\(0<m(a)≦\displaystyle\frac{\sqrt{3}}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→最大・最小値と係数決定 back→極値と条件