最大値・最小値に関する係数決定の例題です。
(例題)
\(a,b\)は正の定数とする。関数
\(y=x+\sqrt{a-bx^2}\)
の最大値が\(2\)、最小値が\(-\sqrt{3}\)となるように\(a,b\)の値を求めよ。
(解答)
\(f(x)=x+\sqrt{a-bx^2}\) とおく。
\(f(x)\)の定義域は、\(a-bx^2≧0\) より
\(-\sqrt{\displaystyle\frac{a}{b}}≦x≦\sqrt{\displaystyle\frac{a}{b}}\)
\(x≠±\sqrt{\displaystyle\frac{a}{b}}\) のとき
\(f'(x)=1+\displaystyle\frac{-2bx}{2\sqrt{a-bx^2}}\)
\(=\displaystyle\frac{\sqrt{a-bx^2}-bx}{\sqrt{a-bx^2}}\)・・・①
(ア)\(-\sqrt{\displaystyle\frac{a}{b}}<x≦0\) のとき
①より \(f'(x)>0\)
(イ)\(0<x<\sqrt{\displaystyle\frac{a}{b}}\) のとき
\(bx=\sqrt{b^2x^2}\) とみてルートの中身を比較してもよいですが、今回は有理化していきます。
①より
\(f'(x)=\displaystyle\frac{(a-bx^2)-(bx)^2}{\sqrt{a-bx^2}\cdot(\sqrt{a-bx^2}+bx)}\)
\(=\displaystyle\frac{a-b(b+1)x^2}{\sqrt{a-bx^2}\cdot(\sqrt{a-bx^2}+bx)}\) (分母は正の値)
\(f'(x)=0\) となるのは
\(a-b(b+1)x^2=0\) より
\(x=\sqrt{\displaystyle\frac{a}{b(b+1)}}\) (定義域内にある)
以上より増減表は次のようになる。
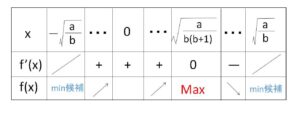
よって最大値は
\(f(\sqrt{\displaystyle\frac{a}{b(b+1)}})=\sqrt{\displaystyle\frac{a}{b(b+1)}}+\sqrt{a-\displaystyle\frac{a}{b+1}}\)
\(=\sqrt{\displaystyle\frac{a}{b(b+1)}}+\sqrt{\displaystyle\frac{ab}{b+1}}\)
\(=\sqrt{\displaystyle\frac{a}{b+1}}\cdot(\displaystyle\frac{1}{\sqrt{b}}+\sqrt{b})\)
\(=\sqrt{\displaystyle\frac{a}{b+1}}\cdot\displaystyle\frac{1+b}{\sqrt{b}}\)
\(=\sqrt{\displaystyle\frac{a(b+1)}{b}}\)
最小値については
\(f(-\sqrt{\displaystyle\frac{a}{b}})=-\sqrt{\displaystyle\frac{a}{b}}\)、 \(f(\sqrt{\displaystyle\frac{a}{b}})=\sqrt{\displaystyle\frac{a}{b}}\)
より
最小値 \(-\sqrt{\displaystyle\frac{a}{b}}\)
ゆえに
\(\sqrt{\displaystyle\frac{a(b+1)}{b}}=2\)・・・②
\(-\sqrt{\displaystyle\frac{a}{b}}=-\sqrt{3}\)・・・③
(あとは連立方程式②③より\(a,b\)を求めるだけ)
③より
\(\displaystyle\frac{a}{b}=3\)・・・④
これを②に代入して
\(\sqrt{3(b+1)}=2\)
よって \(b=\displaystyle\frac{1}{3}\)
④より \(a=1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→最大・最小値と図形問題 back→最大・最小値