媒介変数表示されたグラフの書き方について見ていきます。
(例題1)
\(x=\cos2θ+2\cosθ\)、 \(y=\sin2θ+2\sinθ\) (\(-π≦θ≦π\)) で表される曲線の概形を描け。(凹凸は調べなくてよい)
(2)消去不可ならば、\(x,y\)それぞれを(媒介変数で)微分して、\(x,y\)の変化の仕方を調べてグラフを描きます。ただし、対称性が分かるなら媒介変数の範囲の1部分だけを考えることになるので処理が楽になります。
媒介変数表示の増減表は \(θ(媒介変数),x’,x,y’,y\) の5段式になります。これで大体の場合は十分ですがよりグラフを正確に書くために、\(\displaystyle\frac{dy}{dx},\displaystyle\frac{d^2y}{dx^2}\) を考えることもあります。
(解答)
対称性についてですが、\(x\)が\(\cos\)のみ、\(y\)が\(\sin\)のみの式で表されていることと、\(\cos(-θ)=\cosθ\)、\(\sin(-θ)=-\sinθ\) より、\(x\)軸対称であることが分かります。(詳しくは後述)
\(x=f(θ)=\cos2θ+2\cosθ\)
\(y=g(θ)=\sin2θ+2\sinθ\)
とおく。(\(-π≦θ≦π\))
\(f(θ)=f(-θ)\)、\(g(θ)=-g(-θ)\) だから、この曲線は\(x\)軸対称。したがって \(0≦θ≦π\) の範囲で考えればよい。
また、\(g(θ)=-g(-θ)\) より \(θ=α\) と \(θ=-α\) のときの\(y\)座標は符号が反対で絶対値は同じです。
よって、曲線上には 点\((x,y)\) (\(θ=α\)) に対応する 点\((x,-y)\) (\(θ=-α\)) が存在するために、\(x\)軸対称になります。
また
\(x’=f'(θ)=-2\sin2θ-2\sinθ\)
\(=-4\sinθ\cosθ-2\sinθ\)
\(=-2\sinθ(2\cosθ+1)\)
\(0≦θ≦π\) の範囲では、\(-2\sinθ≦0\) で
\(2\cosθ+1=0\) となるのは、\(θ=\displaystyle\frac{2}{3}π\)
\(y’=g'(θ)=2\cos2θ+2\cosθ\)
\(=2(2\cos^2θ-1)+2\cosθ\)
\(=2(2\cos^2θ+\cosθ-1)\)
\(=2(\cosθ+1)(2\cosθ-1)\)
\(0≦θ≦π\) の範囲では、\(2(\cosθ+1)≧0\) で
\(2\cosθ-1=0\) となるのは、\(θ=\displaystyle\frac{1}{3}π\)
よって増減表は次の通り。
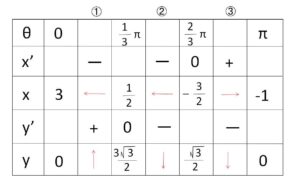
\(θ\)が \(0→π\) と動くときに曲線はどのように描かれるかというと
①\(0→\displaystyle\frac{π}{3}\): 「\(x\)は減少、\(y\)は増加だから左上向きに動く」
②\(\displaystyle\frac{π}{3}→\displaystyle\frac{2}{3}π\): 「\(x\)は減少、\(y\)は減少だから左下向きに動く」
③\(\displaystyle\frac{2}{3}π→π\): 「\(x\)は増加、\(y\)は減少だから右下向きに動く」
あとはこれを\(x\)軸について折り返すと完成です。
したがって曲線は次のようになる。
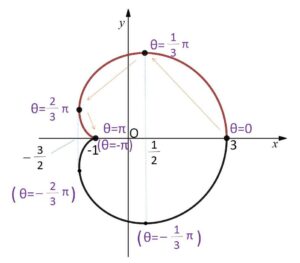
(例題2)
\(x=\displaystyle\frac{t^2}{2}+\displaystyle\frac{1}{t}\)、\(y=t-\displaystyle\frac{t^4}{4}\) (\(t>0\)) で表される曲線の概形を描け。
(解答)
\(x=\displaystyle\frac{t^2}{2}+\displaystyle\frac{1}{t}\)
\(y=t-\displaystyle\frac{t^4}{4}\)
(\(t>0\))
\(x’\)\(=t-\displaystyle\frac{1}{t^2}\)\(=\displaystyle\frac{t^3-1}{t^2}\)
\(y’=1-t^3\)
\(t^3-1=0\) を満たす実数\(t\)は
\((t-1)(t^2+t+1)=0\)
より、\(t=1\)
\(x,y\)について、\(t \to +0\)、\(t \to \infty\) の極限も踏まえると、増減表は次のようになる。
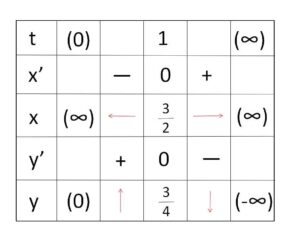
また
\(\displaystyle\frac{dy}{dx}=\displaystyle\frac{y’}{x’}=-t^2\ (<0)\)
より、\(t>0\)の範囲では\(t\)が大きいほど接線の傾きが小さくなるので、曲線は自身で交点をもたない。
なお、\(t=1\) で \(x,y\) の両方が極値となっているので、ここでのグラフは尖った形になります。
よって、グラフの概形は次の通り。
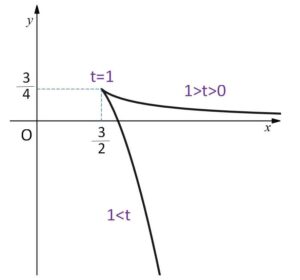
(参考)
増減表だけだと、次のように曲線自身で交点をもつ場合も考えられます。
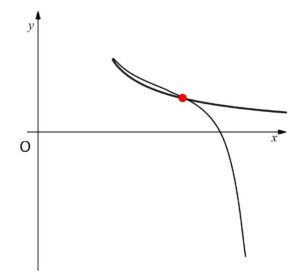
解答ではこの可能性を排除するために接線の傾きの変化を考えましたが、他には
・グラフの凹凸で判断する
・交点を最初から求める (\(x(t_1)=x(t_2)\)、\(y(t_1)=y(t_2)\) を満たす異なる\(t_1,t_2\)があるか調べる)
・同じ\(x\)座標について、\(y\)座標が異なるか調べる (2つ目の方法に近い)
のような方法があります。本問ではグラフの凹凸を考えると
\(\displaystyle\frac{d^2y}{dx^2}=\displaystyle\frac{d}{dx}(\displaystyle\frac{dy}{dx})=\displaystyle\frac{d}{dt}(\displaystyle\frac{dy}{dx})\cdot\displaystyle\frac{dt}{dx}\) (合成関数の微分、\(t\)で仲介)
\(=\displaystyle\frac{d}{dt}(\displaystyle\frac{dy}{dx})\cdot\displaystyle\frac{1}{\displaystyle\frac{dx}{dt}}\) (逆関数の微分)
(\(\displaystyle\frac{dy}{dx}=-t^2\)、\(x’=\displaystyle\frac{t^3-1}{t^2}\) より)
\(=(-2t)\cdot\displaystyle\frac{t^2}{t^3-1}\)
\(=\displaystyle\frac{-2t^3}{t^3-1}\)
より、
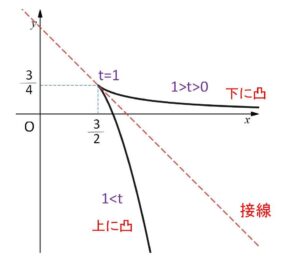
\(0<t<1\) のとき 下に凸
\(t>1\) のとき 上に凸
となります。また \(t=1\) のときの接線は \(\displaystyle\frac{dy}{dx}=-1^2\) より
\(y=-(x-\displaystyle\frac{3}{2})+\displaystyle\frac{3}{4}\)
なので、この接線の上側に \(0<t<1\) の曲線、下側に \(t>1\) の曲線が存在するために、曲線は自身で交わらないことになります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→不等式の証明(1変数) back→陰関数とグラフの概形