数Ⅲの微分を利用する、軌跡と領域に関する例題です。
数Ⅱの知識にプラスして数Ⅲの微分を使うだけなので、特に目新しいことはないです。
(例題1)
実数\(θ\)が動くとき、\(xy\)平面上の動点 \(P(0,\sinθ)\) および \(Q(8\cosθ,0)\) を考える。\(θ\)が \(0≦θ≦\displaystyle\frac{π}{2}\) の範囲を動くとき、平面内で線分\(PQ\)が通過する部分を図示せよ。
その際、分母が\(0\)になる \(θ=\displaystyle\frac{π}{2}\) は別に考えます。
基本的には数式処理で何とかなりますが、実際に線分がどう動いて通過領域がどうなるかを合わせて考えるとよいと思います。
(解答)
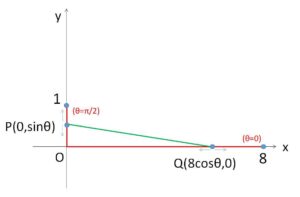
(ア)\(θ=\displaystyle\frac{π}{2}\) のとき
\(P(0,1)\)、\(Q(0,0)\) だから
線分\(PQ\)は \(x=0\) の \(0≦y≦1\) の部分。
(イ)\(0≦θ<\displaystyle\frac{π}{2}\) のとき
線分\(PQ\)の方程式は
\(y=\displaystyle\frac{-\sinθ}{8\cosθ}x+\sinθ\) (\(0≦x≦8\cosθ\))・・・①
\((\sinθ)x+(8\cosθ)y-8\sinθ\cosθ=0\)
となりが、逆像法で「解\(θ\)をもつ\(x,y\)の条件」と解こうとすると、三角関数の種類がまとめられないことが原因でうまくいきません。
よって、順像法で 「\(x=k\) と固定して\(θ\)を動かして\(y\)の範囲を求めて」解くことになります。この際、\(x=0\) と \(x=8\) は特殊な動きになるので分けておきます。
(\(x=8\) は点のみ、\(x=0\) は \(0≦θ<\displaystyle\frac{π}{2}\) で動かすと、\(0≦y<1\) (\(0\)スタートで\(1\)のギリギリまで近づくが、これは(ア)に含まれる))
(i)\(0<x<8\) のとき
①で \(x=k\) (\(0<k<8\)) と固定すると
\(y=-\displaystyle\frac{\tanθ}{8}k+\sinθ\ (=f(θ))\) (\(0<k≦8\cosθ\))
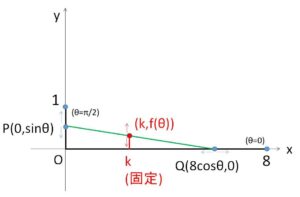
(\(θ\)を変化させたときの増減を考えるので、不等式を\(θ\)基準にしておく。この際 \(k=8\cosθ\) は具体的に解けないので、この解を \(θ=α\) と文字で表しておく)
\(k=8\cosθ\) を満たす\(θ\)を\(α\)とおくと
\(\cosα=\displaystyle\frac{k}{8}\) (\(0<α<\displaystyle\frac{π}{2}\))
また
\((0<)\ \displaystyle\frac{k}{8}≦\cosθ\) となるから、\(θ\)の範囲は
\(0≦θ≦α\)
\(\displaystyle\frac{1}{2}≦\cosθ\) です。このとき \(α=\displaystyle\frac{π}{3}\) で、\(0≦θ≦\displaystyle\frac{π}{3}\) が\(θ\)の動かす範囲です。
この制限を図で対応させると、\(θ=\displaystyle\frac{π}{3}\) のとき線分\(PQ\)の右端\(Q\)がちょうど \((4,0)\) に来て、これ以上\(θ\)を大きくすると、\(Q\)が左に動いて過ぎ去ってしまうので、線分が通過することが無いということです。(線分ではなく直線だとこの制限を検討する必要が無いので難易度は下がります)
(あとは\(f(θ)\)の増減を考えるだけです)
\(f(θ)=-\displaystyle\frac{\tanθ}{8}k+\sinθ\) (\(0≦θ≦α\))
\(f'(θ)=-\displaystyle\frac{k}{8\cos^2θ}+\cosθ=\displaystyle\frac{-k+8\cos^3θ}{\cosθ}\)
ここで、\(\cosθ=\sqrt[3]{\displaystyle\frac{k}{8}}\) を満たす\(θ\)を\(β\)とおくと、
\(\cosβ=\sqrt[3]{\displaystyle\frac{k}{8}}\)
\(0<k<8\) のとき
\(0<β<\displaystyle\frac{π}{2}\)
\(\displaystyle\frac{k}{8}<\sqrt[3]{\displaystyle\frac{k}{8}}\) だから (\(0\)から\(1\)の間の数なので、3乗根をとると大きくなる)
\(\cosα<\cosβ\)
よって
\(0<β<α\) (\(\cos\)だと不等号が逆向きになる)
\(f(0)=0\)
\(f(α)=-\displaystyle\frac{\tanα}{8}\cdot8\cosα+\sinα=0\)
に注意すると、\(f(θ)\) の増減表は次のようになる。
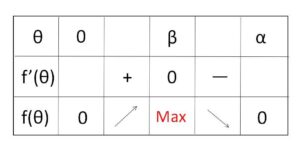
\(f(β)=-\displaystyle\frac{\tanβ}{8}k+\sinβ\)
\(=\sinβ(1-\displaystyle\frac{k}{8\cosβ})\)
\(=\sinβ(1-\displaystyle\frac{8\cos^3β}{8\cosβ})\)
\(=\sinβ(1-\cos^2β)\)
\(=\sin^3β\)
(最後に\(x \ (k)\) で表すために\(β\)を消去)
\(=\left\{\sqrt{1-(\sqrt[3]{\displaystyle\frac{k}{8}})^2}\right\}^3\)
だから
\(0≦f(θ)≦(1-\displaystyle\frac{1}{4}k^{\frac{2}{3}})^{\frac{3}{2}}\)
\(k\)を\(x\)に戻すと、\(0<x<8\) における通過領域は
\(0≦y≦(1-\displaystyle\frac{1}{4}x^{\frac{2}{3}})^{\frac{3}{2}}\)・・・②
(ii)\(x=0,8\) のとき
\(x=8\) では、線分の通過領域は 点\((8,0)\) のみ
これは②で\(x=8\)とすればよい。
\(x=0\) では、線分の通過領域は
\(0≦y<1\) で、(ア)の \(0≦y≦1\) に含まれる。
またこれは②で \(x=0\) とすればよい。
以上より線分の通過する範囲は
\(0≦y≦(1-\displaystyle\frac{1}{4}x^{\frac{2}{3}})^{\frac{3}{2}}\) (\(0≦x≦8\))
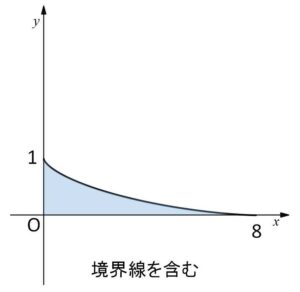
(式から境界の関数は単調減少であることは分かりますが、不安なら微分してください)
(例題2)
定数\(a\)に対して、次の式で定義される\(xy\)平面の曲線を\(C_a\)とする。
\(C_a:y=(a-x)\{\log(x-a)-2\}\)
(1)\(a=0\) のときの曲線\(C_a\)のグラフをかけ。ただし、\(\displaystyle\lim_{x \to \infty}xe^{-x}=0\) を用いてもよい。
(2)\(a\)を \(a≧0\) の範囲で動かすとき、曲線\(C_a\)が通る部分を図示せよ。
(解答)
(1)
\(a=0\) のとき
\(y=-x(\log x-2)\)
\(x>0\) が定義域で
\(y’=-(\log x-2)-x\cdot\displaystyle\frac{1}{x}\)
\(=1-\log x\)
よって増減表は次の通り。
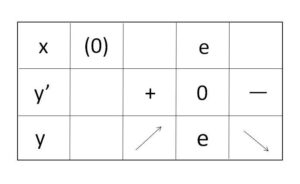
\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{x}{e^x}=0\) は指数関数のほうが発散が強いというよく使う式です。
\(\displaystyle\lim_{x \to +0}\{-x(\log x-2)\}\)
\(=\displaystyle\lim_{x \to +0}\{-x\log x+2x\}\)
ここで
\(\displaystyle\lim_{x \to +0}(-x\log x)\)
\(=\displaystyle\lim_{t \to \infty}-e^{-t}\cdot(-t)\) (\(x=e^{-t}\))
\(=\displaystyle\lim_{t \to \infty}te^{-t}\)
\(=0\)
だから
\(\displaystyle\lim_{x \to +0}\{-x(\log x-2)\}=0\)
また、
\(\displaystyle\lim_{x \to \infty}\{-x(\log x-2)\}=-\infty\) (\(-\infty×\infty\))
したがってグラフは次のようになる。
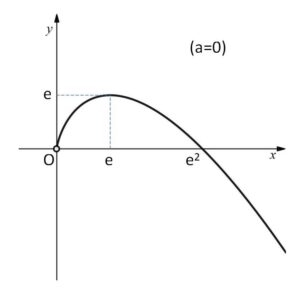
(2)
\(C_a:y=(a-x)\{\log(x-a)-2\}\)
\(=-(x-a)\{\log(x-a)-2\}\)
よって曲線\(C_a\)は(1)の曲線
\(y=-x(\log x-2)\)
を\(x\)軸方向に\(a\)だけ平行移動したものになる。
ゆえに \(a≧0\) において\(C_a\) が通過する部分は、(1)の曲線が原点を含まないことに注意すると、図のようになる。(境界のうち \(x\)軸上の \(0≦x<e^2\) の部分は除く)
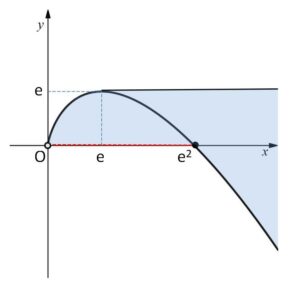
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→関数方程式と微分 back→数値の大小