関数方程式と微分に関する例題です。
(例題1)
すべての実数で定義され何回でも微分できる関数\(f(x)\)が
\(f(0)=0\)、\(f'(0)=1\)
を満たし、さらに任意の実数\(a,b\)に対して \(1+f(a)f(b)≠0\) であって
\(f(a+b)=\displaystyle\frac{f(a)+f(b)}{1+f(a)f(b)}\)
を満たしている。
(1)任意の実数\(a\)に対して、\(-1<f(a)<1\) であることを証明せよ。
(2)\(y=f(x)\) のグラフは \(x>0\) で上に凸であることを証明せよ。
また今回は微分可能という条件もついているので、関数方程式を微分することもできます。
(解答)
(1)
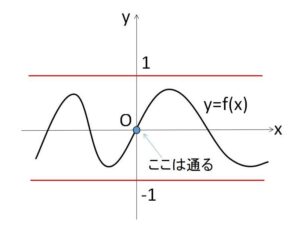
グラフの増減を調べようとして導関数を求めると、\(f(a)\)と\(f'(a)\)の関係式が得られますが、これは(1)ではあまり有益ではないです。((2)で使いますが)
\(f(a+b)=\displaystyle\frac{f(a)+f(b)}{1+f(a)f(b)}\)・・・①
\(f(a)\)は微分可能であるから、連続。
また、\(f(0)=0\) だから、任意の実数\(a\)について \(f(a)≠±1\) であることを示せばよい。
これを背理法で示す。
(ア)
\(f(k)=1\) となる\(k\)が存在すると仮定する。
①で \(b=k\) を代入すると
\(f(a+k)=\displaystyle\frac{f(a)+f(k)}{1+f(a)f(k)}=\displaystyle\frac{f(a)+1}{1+f(a)}=1\)
\(f(a+k)=1\) に \(a=-k\) を代入して
\(f(0)=1\)
これは、\(f(0)=0\) に矛盾するので、\(f(k)=1\) となる\(k\)は存在しない。
(イ)
\(f(k)=-1\) となる\(k\)が存在すると仮定する。
同様に①で \(b=k\) を代入すると
\(f(a+k)=\displaystyle\frac{f(a)+f(k)}{1+f(a)f(k)}=\displaystyle\frac{f(a)-1}{1-f(a)}=-1\)
これに \(a=-k\) を代入して
\(f(0)=-1\)
これは \(f(0)=0\) に矛盾するので、\(f(k)=-1\) となる\(k\)は存在しない。
以上より、任意の実数\(a\)について \(f(a)≠±1\) であるから、\(f(0)=0\) と \(f(a)\)の連続性から題意は示された。
(2)
微分の定義でやっても、関数方程式を微分してもどちらもでよいです。
\(f(a+b)=\displaystyle\frac{f(a)+f(b)}{1+f(a)f(b)}\)・・・①
\(f'(a)=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}\)
について分子は、①で \(b=h\) を代入すると
\(f(a+h)-f(a)=\displaystyle\frac{f(a)+f(h)}{1+f(a)f(h)}-f(a)\)
\(=\displaystyle\frac{f(h)\{1-(f(a))^2\}}{1+f(a)f(h)}\)
よって
\(f'(a)=\displaystyle\lim_{h \to 0}\displaystyle\frac{1-(f(a))^2}{1+f(a)f(h)}\cdot\displaystyle\frac{f(h)}{h}\)
右側は \(\displaystyle\frac{0}{0}\) の不定形なので、これは \(f'(0)=1\) から求めておきます。
ここで
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(h)}{h}=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(h)-f(0)}{h}\) (\(f(0)=0\) より)
\(=f'(0)=1\)
\(f(x)\)の連続性から、\(\displaystyle\lim_{h \to 0}f(h)=f(0)=0\) だから
\(f'(a)=\displaystyle\frac{1-(f(a))^2}{1+0}\cdot1\)
ゆえに
\(f'(a)=1-(f(a))^2\)・・・②
②の両辺を微分して
\(f”(a)=-2f(a)f'(a)\)・・・③
(1)の結果 \(-1<f(a)<1\) と②より
\(f'(a)>0\)
\(f(a)\) は単調増加関数で \(f(0)=0\) より、
\(a>0\) において \(f(a)>0\)
したがって③より \(a>0\) において
\(f”(a)<0\)
つまり \(y=f(x)\) のグラフは、\(x>0\) において上に凸である。
(別解)関数方程式を微分する方法
\(f(a+b)=\displaystyle\frac{f(a)+f(b)}{1+f(a)f(b)}\)・・・①
\(a\)を固定して\(b\)で微分すると
\(f'(a+b)=\displaystyle\frac{f'(b)\{1+f(a)f(b)\}-\{f(a)+f(b)\}f(a)f'(b)}{\{1+f(a)f(b)\}^2}\)
整理すると
\(f'(a+b)=\displaystyle\frac{\{1-(f(a))^2\}f'(b)}{\{1+f(a)f(b)\}^2}\)
\(b=0\) を代入して
\(f'(a)=\displaystyle\frac{\{1-(f(a))^2\}f'(0)}{\{1+f(a)f(0)\}^2}\)
\(f(0)=0\)、\(f'(0)=1\) より
\(f'(a)=1-(f(a))^2\)・・・② (どの実数\(a\)についても成り立つ等式となる)
(以下同様)
(例題2)
関数\(f(x)\)が次の条件 (i),(ii) をみたしている。
(i)任意の実数\(x,y\)について
\(f(x+y)=\displaystyle\frac{f(x)+f(y)}{1+f(x)f(y)}\)、\(1+f(x)f(y)≠0\)
(ii)
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{f(x)}{x}=1\)
(1)\(-\infty<x<\infty\) で \(f(x)\) は微分可能であることを示せ。
(2)\(f(x)\) は奇関数であることを示せ。
(3)\(f(x)\) は増加関数であることを示せ。
(解答)
(1)
(微分の定義より、極限値が存在することを示せばよい)
\(f(x+y)=\displaystyle\frac{f(x)+f(y)}{1+f(x)f(y)}\)・・・①
①に \(y=h\) を代入して
\(f(x+h)=\displaystyle\frac{f(x)+f(h)}{1+f(x)f(h)}\)
よって
\(f(x+h)-f(x)=\displaystyle\frac{f(x)+f(h)}{1+f(x)f(h)}-f(x)\)
\(=\displaystyle\frac{\{1-(f(x))^2\}f(h)}{1+f(x)f(h)}\)
だから
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(x+h)-f(x)}{h}\)
\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(h)}{h}\cdot\displaystyle\frac{1-(f(x))^2}{1+f(x)f(h)}\)
ここで
\(\displaystyle\lim_{h \to 0}f(h)=\displaystyle\lim_{h \to 0}\displaystyle\frac{f(h)}{h}\cdot h=1\cdot0=0\)・・・(※)
だから
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(x+h)-f(x)}{h}\)
\(=1\cdot\displaystyle\frac{1-(f(x))^2}{1+0}\)
\(=1-(f(x))^2\) (収束し、極限値が存在)・・・(注)
したがって \(-\infty<x<\infty\) で \(f(x)\) は微分可能で(これより連続であることも分かる)
\(f'(x)=1-(f(x))^2\)・・・②
が成り立つ。
任意の\(x,y\)について関数方程式(i)が成り立つので、\(f(x)\)の定義域は実数全体で、\(f(x)\)は有限な値です。
(2)
\(f(x+y)=\displaystyle\frac{f(x)+f(y)}{1+f(x)f(y)}\)・・・①
①に \(y=-x\) を代入して
\(f(0)=\displaystyle\frac{f(x)+f(-x)}{1+f(x)f(-x)}\)
ここで(1)より、\(f(x)\)が連続であることから
\(f(0)=\displaystyle\lim_{h \to 0}f(h)=0\) ((1)の※より)
したがって
\(0=f(x)+f(-x)\)
\(f(x)=-f(-x)\) (奇関数)
(3)
(1)(2)より
\(f'(x)=1-(f(x))^2=1-f(x)\cdot(-f(-x))\)
\(=1+f(x)f(-x)\)
よって条件(ii)の後半より
\(f'(x)≠0\)
よって、\(f'(x)\)が\(0\)にならないことから、\(f'(x)<0\) or \(f'(x)>0\) のどちらかになります。増加関数なので、後者になるのでこれを示します。
ここで、\(f(x)\)は連続関数だから
\(f'(x)=1-(f(x))^2\) より \(f'(x)\) は連続関数。
また
\(f'(0)=1-(f(0))^2=1>0\) ((2)の\(f(0)=0\)より)
したがって任意の実数\(x\)で
\(f'(x)>0\) となるから、\(f(x)\)は増加関数となる。
よってこれより得られた式も任意の実数について成り立っています。
(基本的に導かれた等式や不等式は、恒等式・絶対不等式になる)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→凸関数① back→軌跡・領域と微分