下に凸(上に凸)である関数と直線の位置関係について見ていきます。
・凸関数と直線
まずは接線から。
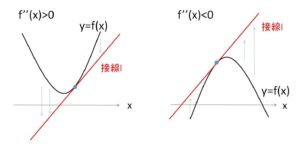
図からも分かりますが、下に凸(上に凸)である関数と接線の位置関係は次のようになります。
2回微分可能な関数\(f(x)\)の接線を\(l\)とすると、\(y=f(x)\) と \(l\) のグラフの位置関係は
(1)\(f”(x)>0\) (下に凸) のとき、\(f(x)\)の下側に接線\(l\)が位置する。
(2)\(f”(x)<0\) (上に凸) のとき、\(f(x)\)の上側に接線\(l\)が位置する。
(いずれも接点では\(y\)座標は同じになる)
(証明)
(1)のみ証明する。((2)も同様に示せる)
(接線の方程式を立てて、差をとって微分していきます。\(f”(x)>0\) がポイントとなる条件なので、2回微分して増減を調べます)
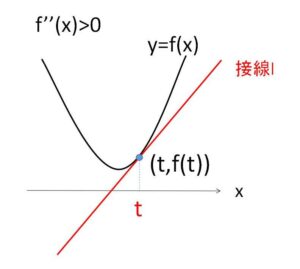
接点の\(x\)座標を\(t\)とおく。
接線の方程式は
\(y=f'(t)(x-t)+f(t)\)
\(F(x)=f(x)-\{f'(t)(x-t)+f(t)\}\) とおくと (\(t\)は定数扱いの\(x\)の関数)
\(F'(x)=f'(x)-f'(t)\)
\(F”(x)=f”(x)>0\)
よって、\(F'(x)\) は単調増加。
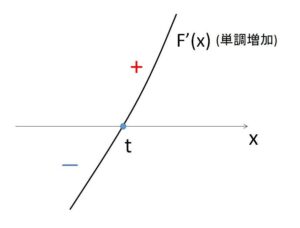
また \(F'(t)=f'(t)-f'(t)=0\) より、
\(x<t\) のとき \(F'(x)<0\)
\(x=t\) のとき \(F'(x)=0\)
\(x>t\) のとき \(F'(x)>0\)
となるから、\(F(x)\) の最小値は
\(F(t)=f(t)-\{0+f(t)\}=0\)
したがって
\(F(x)≧0\)
つまり
\(f(x)≧f'(t)(x-t)+f(t)\) (\(f(x)\)が上側、接線が下側)
(等号は \(x=t\) のみ成立)
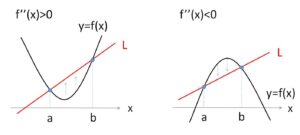
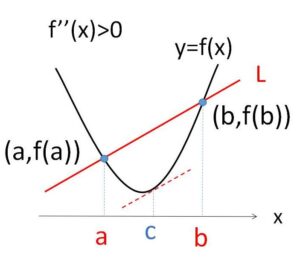
続いて\(f(x)\)と直線が異なる2点で交わる場合です。こちらも図から判断が可能です。
2回微分可能な関数 \(y=f(x)\) 上の異なる2点を通る直線を\(L\)とする。2交点の\(x\)座標を\(a,b\) (\(a<b\)) とすると、\(a<x<b\) の範囲において
(1)\(f”(x)>0\) (下に凸) のとき、\(f(x)\)の上側に直線\(L\)が位置する。
(2)\(f”(x)<0\) (上に凸) のとき、\(f(x)\)の下側に直線\(L\)が位置する。
また、この2交点以外に交点は存在しない。
(証明)
(1)のみ示す。((2)も同様)
(先ほどの接線のときと同様に差をとって2回微分していきます)
2点を通る直線\(L\)の方程式は
\(y=\displaystyle\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\)
\(G(x)=\{\displaystyle\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\}-f(x)\) とおくと
\(G'(x)=\displaystyle\frac{f(b)-f(a)}{b-a}-f'(x)\)
\(G”(x)=-f”(x)<0\)
よって、\(G'(x)\) は単調減少。
また平均値の定理より
\(\displaystyle\frac{f(b)-f(a)}{b-a}=f'(c)\) (\(a<c<b\))
となる\(c\)が存在し、\(G'(c)=0\)
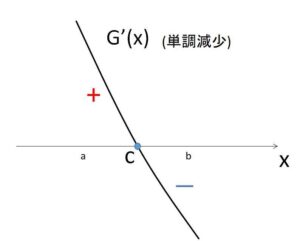
ゆえに
\(x<c\) のとき \(G'(x)>0\) (\(G(x)\)は単調増加)
\(x=c\) のとき \(G'(x)=0\)
\(x>c\) のとき \(G'(x)<0\) (\(G(x)\)は単調減少)
\(G(a)=f(a)-f(a)=0\)
\(G(b)=\{f(b)-f(a)+f(a)\}-f(b)=0\)
も踏まえると、\(y=G(x)\) のグラフは次のようになる。
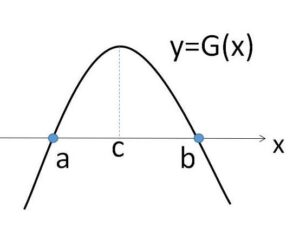
したがって \(a<x<b\) において
\(G(x)>0\)
つまり
\(\displaystyle\frac{f(b)-f(a)}{b-a}(x-a)+f(a)>f(x)\) (直線が上側、\(f(x)\)が下側)
またグラフより他に交点が存在しないことも分かる。
なお2交点の線分の内分点に着目した別の表現方法もありますが、これは次回に扱いたいと思います。
(例題)
実数\(a,b\) (\(0≦a<\displaystyle\frac{π}{4}\)、\(0≦b<\displaystyle\frac{π}{4}\)) に対し次の不等式が成り立つことを示せ。
\(\sqrt{\tan a\tan b}≦\tan\displaystyle\frac{a+b}{2}≦\displaystyle\frac{1}{2}(\tan a+\tan b)\)
\(a=b\) と \(a≠b\) のときで事情が違ってくるので場合分けします。\(a≠b\) については、条件と証明したい不等式が\(a,b\)を入れ替えても変わらないので(対称性がある)、\(a<b\) と設定しても問題なく、これで話を進めていきます。
中辺と右辺が座標平面で図形的に何を表しているかというと、\(y=\tan x\) を考えれば、
(右辺)は「2交点の中点の\(y\)座標」、(中辺)は「2交点の中点の\(x\)座標における \(y=\tan x\) の値」です。すると上下関係から不等式が成り立つことが見えてきます。
左辺と中辺については、対数をとると同じ議論ができます。(\(a=0\)、\(b=0\) は別にする必要があります)
(解答)
\(\sqrt{\tan a\tan b}≦\tan\displaystyle\frac{a+b}{2}≦\displaystyle\frac{1}{2}(\tan a+\tan b)\)・・・①
(\(0≦a<\displaystyle\frac{π}{4}\)、\(0≦b<\displaystyle\frac{π}{4}\))
を証明したい。
\(a=b\) のとき
\(\sqrt{\tan a\tan b}=\tan a\)
\(\tan\displaystyle\frac{a+b}{2}=\tan a\)
\(\displaystyle\frac{1}{2}(\tan a+\tan b)=\tan a\)
となるので、不等式①が成り立つ。
\(a≠b\) のとき
対称性から、\(a<b\) としても一般性を失わない。
(i)まず、①の (中辺)\(≦\)(右辺) について
\(f(x)=\tan x\) (\(0≦x<\displaystyle\frac{π}{4}\)) とおくと
\(f'(x)=\displaystyle\frac{1}{\cos^2x}\)
\(f”(x)=\displaystyle\frac{-2(-\sin x)}{\cos^3x}=\displaystyle\frac{2\sin x}{\cos^3x}≧0\) (等号は\(x=0\)のみ)
(1点だけで\(f”(x)=0\)となる場合も、上で説明した内容は成り立ちます。不安なら\(a=0\)のときで場合分けして下さい)
よって、\(y=f(x)\) は下に凸のグラフ。
\(A(a,f(a))\)、\(B(b,f(b))\) とおくと、線分\(AB\)の中点\(M\)は
\(M(\displaystyle\frac{a+b}{2},\displaystyle\frac{f(a)+f(b)}{2})\)
また点\(N\)を、\(x=\displaystyle\frac{a+b}{2}\) における \(y=f(x)\) 上の点とすると
\(N(\displaystyle\frac{a+b}{2},f(\displaystyle\frac{a+b}{2}))\)
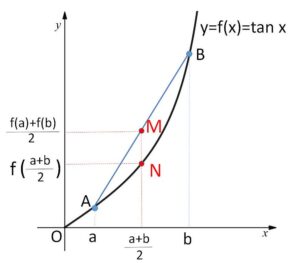
図より\(N\)ほうが下側にあるので
\(f(\displaystyle\frac{a+b}{2})<\displaystyle\frac{f(a)+f(b)}{2}\)
ゆえに
\(\tan\displaystyle\frac{a+b}{2}<\displaystyle\frac{1}{2}(\tan a+\tan b)\)
(ii)次に①の (左辺)\(≦\)(中辺) について
\(a=0\) のときは
(左辺)=\(0\)
(中辺)=\(\tan\displaystyle\frac{b}{2}>0\) より不等式は成り立つ。
\(0<a<b<\displaystyle\frac{π}{4}\) のとき、不等式で対数をとると
\(\log(\sqrt{\tan a\tan b})≦\log(\tan\displaystyle\frac{a+b}{2})\)
となるから
\(\displaystyle\frac{1}{2}(\log\tan a+\log\tan b)≦\log(\tan\displaystyle\frac{a+b}{2})\)
を示せばよい。
\(g(x)=\log(\tan x)\) (\(0<x<\displaystyle\frac{π}{4}\)) とおくと
\(g'(x)=\displaystyle\frac{1}{\tan x}\cdot\displaystyle\frac{1}{\cos^2 x}=\displaystyle\frac{1}{\sin x\cos x}\)
\(=\displaystyle\frac{2}{\sin2x}\)
\(g”(x)=\displaystyle\frac{-2}{\sin^22x}\cdot(2\cos2x)=\displaystyle\frac{-4\cos2x}{\sin^22x}<0\)
よって \(y=g(x)\) のグラフは上に凸。
(i)と同様に考えると、今度は線分\(AB\)が \(y=g(x)\) のグラフより下側にあるので
\(\displaystyle\frac{g(a)+g(b)}{2}<g(\displaystyle\frac{a+b}{2})\)
ゆえに
\(\displaystyle\frac{1}{2}(\log\tan a+\log\tan b)<\log(\tan\displaystyle\frac{a+b}{2})\)
したがって
\(\sqrt{\tan a\tan b}<\tan\displaystyle\frac{a+b}{2}\)
が成り立つ。
以上より題意は示された。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→凸関数② back→関数方程式と微分