凸関数の演習です。
(例題1)
(1)\(a,b\)を異なる実数とし、関数\(f(x)\)が\(a,b\)を含む区間で第2次導関数\(f”(x)\)を持ち、\(f”(x)<0\) が成り立つものとする。このとき \(0≦t≦1\) に対して
\(tf(a)+(1-t)f(b)≦f(ta+(1-t)b)\)
が成り立つことを示せ。
(2)\(f(x)=\log x\) に(1)の結果を適用することにより、正の数\(a,b,c\) に対して、
\(\sqrt[3]{abc}≦\displaystyle\frac{a+b+c}{3}\)
が成り立つことを示せ。ただし、\(\log x\) は自然対数とする。
(解答)
(1)
前回と同じように、1文字固定で微分して証明したいと思います。
\(b\)を固定し、\(a\)の関数とみて
\(F(x)=f(tx+(1-t)b)-\{tf(x)+(1-t)f(b)\}\)
とおく。\(x\)で微分して
\(F'(x)=t\{f'(tx+(1-t)b)-f'(x)\}\)
\(f”(x)<0\) より、\(f'(x)\) は減少関数。
このことと
\(tx+(1-t)b-x=(1-t)b-(1-t)x=(1-t)(b-x)\)
と、\(0≦t≦1\) より
(関数の中身が小さいほうが関数の値としては大きくなるから)
\(x<b\) のとき \(f'(tx+(1-t)b)-f'(x)≦0\)
\(x>b\) のとき \(f'(tx+(1-t)b)-f'(x)≧0\)
つまり
\(x<b\) のとき \(F'(x)≦0\)
\(x>b\) のとき \(F'(x)≧0\)
よって\(F(x)\)の最小値は
\(F(b)=f(b)-f(b)=0\)
となるから、\(x≠b\) のとき \(F(x)≧0\)
(\(a,b\)は異なる数なので、\(x≠b\) だが \(t=0,1\) のときは常に \(F'(x)=0\) となるので等号がつく)
\(x\)を\(a\)に戻すと
\(tf(a)+(1-t)f(b)≦f(ta+(1-t)b)\)
(2)
文字が\(a,b,c\)の3つあるので、2段階に分けて不等式を証明することになります。
目標の不等式で対数をとると
\(\displaystyle\frac{f(a)+f(b)+f(c)}{3}≦f(\displaystyle\frac{a+b+c}{3})\)
となるのでこの右辺になるように、(1)で \(t=\displaystyle\frac{1}{3}\)、\(a\)はそのまま、\(b=\displaystyle\frac{b+c}{2}\) とすると
\(\displaystyle\frac{1}{3}f(a)+\displaystyle\frac{2}{3}f(\displaystyle\frac{b+c}{2})≦f(\displaystyle\frac{a+b+c}{3})\)
となります。あとは左辺の \(f(\displaystyle\frac{b+c}{2})\) の部分にもう1回不等式を使うだけです。
(1)より
\(tf(a)+(1-t)f(b)≦f(ta+(1-t)b)\)・・・(※)
(※)で
\(t=\displaystyle\frac{1}{3}\)、\(a\)はそのまま、\(b=\displaystyle\frac{b+c}{2}\) とすると
\(\displaystyle\frac{1}{3}f(a)+\displaystyle\frac{2}{3}f(\displaystyle\frac{b+c}{2})≦f(\displaystyle\frac{a}{3}+\displaystyle\frac{2}{3}\cdot\displaystyle\frac{b+c}{2})\)
つまり
\(\displaystyle\frac{1}{3}f(a)+\displaystyle\frac{2}{3}\color{blue}{f(\displaystyle\frac{b+c}{2})}≦f(\displaystyle\frac{a+b+c}{3})\)・・・①
また(※)で\(t=\displaystyle\frac{1}{2}\)、\(a,b\) を \(b,c\) とすると
\(\displaystyle\frac{f(b)+f(c)}{2}≦\color{blue}{f(\displaystyle\frac{b+c}{2})}\)・・・②
①②より
\(\displaystyle\frac{1}{3}f(a)+\displaystyle\frac{2}{3}\cdot\displaystyle\frac{f(b)+f(c)}{2}≦f(\displaystyle\frac{a+b+c}{3})\)
よって
\(\displaystyle\frac{1}{3}\{f(a)+f(b)+f(c)\}≦f(\displaystyle\frac{a+b+c}{3})\)
ゆえに
\(\displaystyle\frac{1}{3}\log abc≦\log(\displaystyle\frac{a+b+c}{3})\)
\(\log \sqrt[3]{abc}≦\log(\displaystyle\frac{a+b+c}{3})\)
\(\sqrt[3]{abc}≦\displaystyle\frac{a+b+c}{3}\)
同様に\(n\)個の相加相乗平均の不等式も、イェンゼンの不等式で、\(t_1=t_2=\cdots=t_n=\displaystyle\frac{1}{n}\) として、\(f(x)=\log x\) を用いることで
\(\sqrt[n]{x_1x_2\cdots x_n}≦\displaystyle\frac{x_1+x_2+\cdots+x_n}{n}\)
(\(x_1,x_2,\cdots,x_n\) はすべて正の数)
が成り立つことが分かります。
(例題2)
(1)\(f(x)=\log(\sin x)\) (\(0<x<π\)) とするとき、\(f(x)\) のグラフの概形を描け。(凹凸も調べよ)
(2)\(α,β,γ\) は \(α>0\)、\(β>0\)、\(γ>0\)、\(α+β+γ\) を満たすとする。このとき、\(\sinα\sinβ\sinγ\) の最大値を求めよ。
(解答)
(1)
\(f(x)=\log(\sin x)\) (\(0<x<π\))
\(f'(x)=\displaystyle\frac{\cos x}{\sin x}\)
\(\sin x>0\) より、
\(0<x≦\displaystyle\frac{π}{2}\) で単調増加。
\(\displaystyle\frac{π}{2}≦x<π\) で単調減少。
最大値は \(f(\displaystyle\frac{π}{2})=0\)
\(\displaystyle\lim_{x \to +0}f(x)=-\infty\)、\(\displaystyle\lim_{x \to π-0}f(x)=-\infty\) であり
\(f”(x)=\displaystyle\frac{-\sin^2x-\cos^2x}{\sin^2x}=\displaystyle\frac{-1}{\sin^2x}<0\)
だから、グラフは上に凸。
以上のことからグラフの次のようになる。
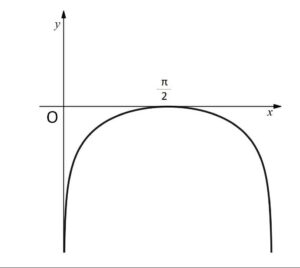
(2)
\(\sinα\sinβ\sinγ\) で対数をとると \(f(α)+f(β)+f(γ)\) となりますが、これを\(\displaystyle\frac{1}{3}\) 倍すると、3点 \((α,f(α))\)、\((β,f(β))\)、\((γ,f(γ))\) で作られる三角形の重心の\(y\)座標となります。グラフは上に凸であることから三角形の重心はグラフの下側にあって、\(\displaystyle\frac{α+β+γ}{3}=\displaystyle\frac{π}{3}\) で一定なので重心の\(x\)座標は固定で、最も重心の\(y\)座標が大きくなるのは、重心がグラフ上にあるときです。(3点が重なるので重心とは言えないかもしれないが)
(1)より、
\(f(x)=\log(\sin x)\) は上に凸のグラフ。
\(\log(\sinα\sinβ\sinγ)\)
\(=f(α)+f(β)+f(γ)\)
であり、グラフ上に3点 \((α,f(α))\)、\((β,f(β))\)、\((γ,f(γ))\) をとると
\((\displaystyle\frac{α+β+γ}{3},\displaystyle\frac{f(α)+f(β)+f(γ)}{3})\)
\(=(\displaystyle\frac{π}{3},\displaystyle\frac{f(α)+f(β)+f(γ)}{3})\)
はこの3点で作られる三角形の重心の座標である。

グラフが上に凸であることから、重心の\(y\)座標はグラフの下側にあるので、点が一致するときも含めると
\(\displaystyle\frac{f(α)+f(β)+f(γ)}{3}≦f(\displaystyle\frac{α+β+γ}{3})\)・・・(※)
(等号成立は3点が重なるときで、\(α=β=γ\))
つまり
\(\displaystyle\frac{1}{3}\log(\sinα\sinβ\sinγ)≦\log(\sin\displaystyle\frac{π}{3})\)
が成り立つ。
よって
\(\log\sqrt[3]{\sinα\sinβ\sinγ}≦\log(\displaystyle\frac{\sqrt{3}}{2})\)
\(\sqrt[3]{\sinα\sinβ\sinγ}≦\displaystyle\frac{\sqrt{3}}{2}\)
\(\sinα\sinβ\sinγ≦\displaystyle\frac{3\sqrt{3}}{8}\)
したがって
\(α=β=γ\) と、\(α+β+γ=π\) より
\(α=β=γ=\displaystyle\frac{π}{3}\) のとき等号が成立するので、このとき
最大値 \(\displaystyle\frac{3\sqrt{3}}{8}\) をとる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→曲線と曲線の距離 back→凸関数②