不等式の成立する定数の値の範囲を求める例題です。
ポイントは「定数分離」です。
(例題1)
\(n\)を自然数とするとき、すべての正の数\(x\)に対して \(\log x+\displaystyle\frac{a}{x^n}>0\) が成り立つための実数\(a\)の範囲を\(n\)を用いて表せ。なお、必要ならば \(\displaystyle\lim_{x \to +0}x\log x=0\) を用いてもよい。
左辺の関数を微分して増減を調べて、\(x\)軸より上側にあるような\(a\)の範囲を・・・とやってもよいですが、定数\(a\)は簡単に分離できるので、不等式を変形して
\(a>-x^n\log x\)
とすると、\(y=a\) が \(y=-x^n\log x\) より上側にある\(a\)の範囲と言い換えることができます。定数分離をすることで、\(y=-x^n\log x\) は固定された関数になっていて、 あとは \(y=a\) を動かすことになりますが、\(y=a\) は\(x\)軸に平行な直線なので、簡単に図から考えることができます。
(解答)
\(\log x+\displaystyle\frac{a}{x^n}>0\)
と、\(x^n>0\) より
\(a>-x^n\log x\)・・・①
\(f(x)=-x^n\log x\) とおくと①より
\(x>0\) の範囲で \(y=f(x)\) のグラフの上側に \(y=a\) のグラフがあるような\(a\)の値の範囲を求めればよい。
\(f'(x)=-nx^{n-1}\log x-x^n\cdot\displaystyle\frac{1}{x}\)
\(=-x^{n-1}(n\log x+1)\)
\(f'(x)=0\) を満たすのは \(x=e^{-\frac{1}{n}}\)
\(\displaystyle\lim_{x \to +0}f(x)=\displaystyle\lim_{x \to +0}-x^{n-1}(x\log x)=0\) も踏まえると、増減表とグラフは次の通り。
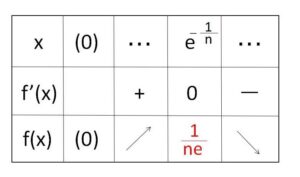
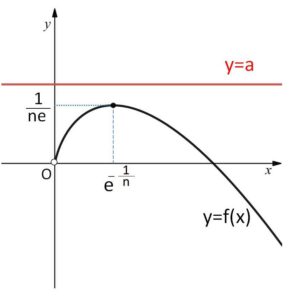
したがって、\(a>f(x)\)・・・① が \(x>0\) を満たす任意の\(x\)について成り立つ\(a\)の値の範囲は
\(a>\displaystyle\frac{1}{ne}\)
(例題2)
すべての正の実数\(x,y\)に対し
\(\sqrt{x}+\sqrt{y}≦k\sqrt{2x+y}\)
が成り立つような実数\(k\)の最小値を求めよ。
関数の増減で考えるなら、まず両辺の次数が同じ(同次形)ことに着目して、\(\sqrt{y}\) で割ると
\(\sqrt{\displaystyle\frac{x}{y}}+1≦k\sqrt{\displaystyle\frac{2x}{y}+1}\)
となり、\(\displaystyle\frac{x}{y}=t\ (>0)\) とおくと
\(\sqrt{t}+1≦k\sqrt{2t+1}\)
となり、1変数に帰着できます。あとは(例題1)と同様に定数分離したいと思います。
(解答)
\(\sqrt{x}+\sqrt{y}≦k\sqrt{2x+y}\)
より、\(\sqrt{y}\)で両辺割って
\(\sqrt{\displaystyle\frac{x}{y}}+1≦k\sqrt{\displaystyle\frac{2x}{y}+1}\)
\(\displaystyle\frac{x}{y}=t\) とおくと、\(x,y\)は正の実数だから \(t>0\) で
\(\sqrt{t}+1≦k\sqrt{2t+1}\)
よって
\(\displaystyle\frac{\sqrt{t}+1}{\sqrt{2t+1}}≦k\)・・・①
が \(t>0\) を満たす任意の\(t\)で成り立つような\(k\)の最小値を求めばよい。
\(f(t)=\displaystyle\frac{\sqrt{t}+1}{\sqrt{2t+1}}\) (\(t>0\)) とおくと
\(f'(t)=\displaystyle\frac{\displaystyle\frac{1}{2\sqrt{t}}\cdot\sqrt{2t+1}-(\sqrt{t}+1)\cdot\displaystyle\frac{2}{2\sqrt{2t+1}}}{2t+1}\)
\(=\displaystyle\frac{1-2\sqrt{t}}{2\sqrt{t}(2t+1)^{\frac{3}{2}}}\)
ゆえに増減表は次の通り。
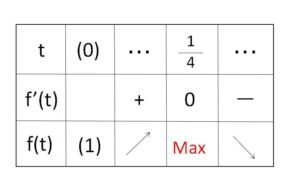
\(f(t)\) の最大値は
\(f(\displaystyle\frac{1}{4})=\displaystyle\frac{\displaystyle\frac{3}{2}}{\sqrt{\displaystyle\frac{3}{2}}}=\)\(\sqrt{\displaystyle\frac{3}{2}}\)
だから、\(f(t)≦k\)・・・① が成り立つような\(k\)の最小値は
\(k=\sqrt{\displaystyle\frac{3}{2}}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→方程式の解の個数 back→不等式と極限②