微分を利用する、方程式の実数解の個数の例題です。
今回も定数分離がポイントになります。
(例題1)
\(f(x)=2x^3+x^2-3\) とおく。直線 \(y=mx\) が曲線 \(y=f(x)\) と相異なる3点で交わるような実数\(m\)の範囲を求めよ。
\(2x^3+x^2-3=mx\) が異なる3つの実数解をもつ\(m\)の条件を求めることになります。左辺に全て寄せて微分をしてもよいですが(計算は大変になる)、定数分離をすると楽です。その際 \(x\) で割ることになるので \(x=0\) が解になるかどうかを確認しておきます。
(解答)
\(2x^3+x^2-3=mx\)・・・①
が異なる3つの実数解をもてばよい。
①に \(x=0\) を代入すると
\(-3=0\) となり、等式が成り立たないので \(x=0\) は解にはならない。
よって \(x≠0\) だから①の両辺を\(x\)で割って
\(2x^2+x-\displaystyle\frac{3}{x}=m\)・・・②
\(g(x)=2x^2+x-\displaystyle\frac{3}{x}\) (\(x≠0\)) とおくと
\(y=g(x)\) と \(y=m\) のグラフが異なる3点で交わればよい。
\(g'(x)=4x+1+\displaystyle\frac{3}{x^2}\)
\(=\displaystyle\frac{4x^3+x^2+3}{x^2}\)
\(=\displaystyle\frac{(x+1)(4x^2-3x+3)}{x^2}\)
ここで \(4x^2-3x+3=0\) の判別式は
\(D=9-48<0\) だから、\(4x^2-3x+3>0\)
よって、\(x+1\) の符号と \(g'(x)\) は一致する。
また、
\(\displaystyle\lim_{x \to -0}g(x)=\displaystyle\lim_{x \to -0}(2x^2+x-\displaystyle\frac{3}{x})=\infty\)
\(\displaystyle\lim_{x \to +0}g(x)=\displaystyle\lim_{x \to +0}(2x^2+x-\displaystyle\frac{3}{x})=-\infty\)
\(\displaystyle\lim_{x \to ±\infty}g(x)=\displaystyle\lim_{x \to ±\infty}x^2(2+\displaystyle\frac{1}{x}-\displaystyle\frac{3}{x^3})=\infty\)
ゆえに \(g(x)\) の増減表とグラフは次のようになる。
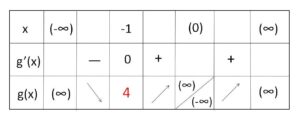
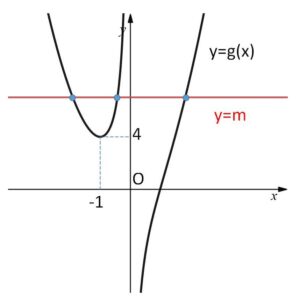
したがって求める\(m\)の範囲は
\(m>4\)
(例題2)
\(k\)を実数の定数とする。方程式
\(4\cos^2x+3\sin x-k\cos x-3=0\)
の \(-π<x≦π\) における解の個数を求めよ。
よって微分を利用することになりますが、今回も定数分離でいきたいとおもいます。
(解答)
\(4\cos^2x+3\sin x-k\cos x-3=0\) (\(-π<x≦π\))
より
\(4\cos^2x+3\sin x-3=k\cos x\)・・・①
(\(\cos x=0\) となる場合を吟味します)
\(\cos x=0\) のとき、\(x=±\displaystyle\frac{π}{2}\)
(ア)\(x=\displaystyle\frac{π}{2}\) のとき
①は
\(0+3-3=k\cdot0\) であり、等式は成り立つ。
よって、\(k\)の値に関わらず \(x=\displaystyle\frac{π}{2}\) は解になる。
(イ)\(x=-\displaystyle\frac{π}{2}\) のとき
①は
\(0-3-3=k\cdot0\) であり、等式は成り立たないので、\(x=-\displaystyle\frac{π}{2}\) は解にならない。
(ウ)\(x≠±\displaystyle\frac{π}{2}\) のとき
①より
\(4\cos x+3\tan x-\displaystyle\frac{3}{\cos x}=k\)
\(f(x)=4\cos x+3\tan x-\displaystyle\frac{3}{\cos x}\) (\(-π<x≦π\))
とおくと、\(y=f(x)\) と \(y=k\) の交点の個数が解の個数となる。
\(f'(x)=-4\sin x+\displaystyle\frac{3}{\cos^2x}-\displaystyle\frac{3\sin x}{\cos^2x}\)
\(=\displaystyle\frac{-4\sin x(1-\sin^2x)+3-3\sin x}{\cos^2x}\)
\(=\displaystyle\frac{4\sin^3x-7\sin x+3}{\cos^2x}\)
\(=\displaystyle\frac{(1-\sin x)(2\sin x+3)(1-2\sin x)}{\cos^2x}\)
よって \(1-2\sin x\) と \(f'(x)\) の符号は一致する。
(\(1-2\sin x=0\) を満たすのは、\(x=\displaystyle\frac{π}{6},\displaystyle\frac{5π}{6}\))
また
\(\displaystyle\lim_{x \to -π+0}f(x)=\displaystyle\lim_{x \to -π+0}(4\cos x+3\tan x-\displaystyle\frac{3}{\cos x})=-1\)
\(\displaystyle\lim_{x \to -\frac{π}{2}-0}f(x)=\displaystyle\lim_{x \to -\frac{π}{2}-0}(4\cos x+\displaystyle\frac{3(\sin x-1)}{\cos x})=\infty\) (\(0+\displaystyle\frac{-6}{-0}\))
\(\displaystyle\lim_{x \to -\frac{π}{2}+0}f(x)=\displaystyle\lim_{x \to -\frac{π}{2}+0}(4\cos x+\displaystyle\frac{3(\sin x-1)}{\cos x})=-\infty\) (\(0+\displaystyle\frac{-6}{+0}\))
\(\displaystyle\lim_{x \to \frac{π}{2}}f(x)=\displaystyle\lim_{x \to \frac{π}{2}}(4\cos x+\displaystyle\frac{3(\sin x-1)}{\cos x})\) (\(0+\displaystyle\frac{0}{0}\) 型なので変形していく)
\(=\displaystyle\lim_{x \to \frac{π}{2}}(4\cos x+\displaystyle\frac{3(-\cos^2x)}{\cos x(\sin x+1)})\)
\(=\displaystyle\lim_{x \to \frac{π}{2}}(4\cos x-\displaystyle\frac{3\cos x}{\sin x+1})\)
\(=0-\displaystyle\frac{0}{2}=0\)
ゆえに増減表とグラフは次の通り。
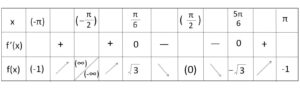
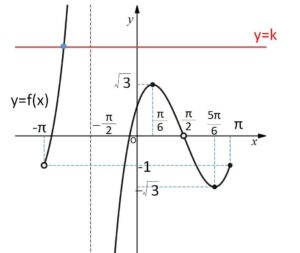
(ア)より、\(x=\displaystyle\frac{π}{2}\) が常に解になるから
「(ウ)によるグラフの交点の個数\(+1\)個」が解の個数になる。
(ウ)において、\(y=f(x)\) の定義域に注意すると (\(x≠-π,±\displaystyle\frac{π}{2}\))
\(k>\sqrt{3}\) のとき 2個
\(k=\sqrt{3}\) のとき 3個
\(0<k<\sqrt{3}\) のとき 4個
\(k=0\) のとき 3個
\(-\sqrt{3}<k<0\) のとき 4個
\(k=-\sqrt{3}\) のとき 3個
\(k<-\sqrt{3}\) のとき 2個
(個数別にまとめてもよい)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線の本数 back→不等式の成立と定数分離