同じ(形の)関数に着目する例題です。
(例題1)
(1)\(n\)を自然数とし、\(e\)を自然対数の底とする。このとき、任意の正の数\(x\)に対して
\(\log x≦\displaystyle\frac{n}{e}x^{\frac{1}{n}}\)
を証明せよ。
(2)\(x>0\) において関数 \(y=\displaystyle\frac{\log x}{x}\) の増減を調べ、そのグラフをかけ。
(3)正の数\(a,b\)が \(a^b=b^a\) および \(a<b\) を満たすとき、\(a\)の範囲を求めよ。
(4)方程式 \(s^t=t^s\) (\(s<t\)) の正の整数解を求めよ。
(解答)
(1)
(基本通り、差をとって微分します)
\(f(x)=\displaystyle\frac{n}{e}x^{\frac{1}{n}}-\log x\) (\(x>0\))
とおくと
\(f'(x)=\displaystyle\frac{x^{\frac{1}{n}-1}}{e}-\displaystyle\frac{1}{x}\)
\(=\displaystyle\frac{1}{ex}(x^{\frac{1}{n}}-e)\)
(\(f'(x)=0\) を満たすのは \(x=e^n\))
よって増減表は次の通り。
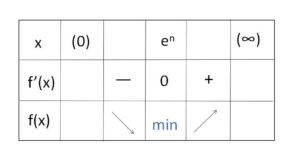
ゆえに\(f(x)\)の最小値は
\(f(e^n)=\displaystyle\frac{n}{e}e-n=0\)
だから
\(f(x)≧0\)
したがって
\(\log x≦\displaystyle\frac{n}{e}x^{\frac{1}{n}}\)
(2)
\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{\log x}{x}\) (\(\displaystyle\frac{\infty}{\infty}\) の不定形)
が必要になってきます。対数より整式の発散が強いことから\(0\)に収束することを知っていればそれでおしまいですが、(1)の誘導も踏まえて、(1)で示した不等式で極限を求めていきます。
なお、\(x \to +0\) の極限は、\(\displaystyle\frac{-\infty}{+0}=-\infty\) です。
\(y=\displaystyle\frac{\log x}{x}\) (\(x>0\))
\(y’=\displaystyle\frac{\displaystyle\frac{1}{x}\cdot x-\log x\cdot1}{x^2}\)
\(=\displaystyle\frac{1-\log x}{x^2}\)
(\(y’=0\) のとき \(x=e\) )
また
\(\displaystyle\lim_{x \to +0}\displaystyle\frac{\log x}{x}=-\infty\)
\(x \to \infty\) については
(1)の不等式で \(n=2\) とすると (\(n≧2\)なら何でもよい)
\(\log x≦\displaystyle\frac{2}{e}\sqrt{x}\)
\(x>1\) (\(\log x>0\)) としてよく、\(x\)で両辺割ると
\(0<\displaystyle\frac{\log x}{x}≦\displaystyle\frac{2}{e\sqrt{x}}\)
はさみうちの原理から
\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{\log x}{x}=0\)
よって増減表とグラフは次の通り。
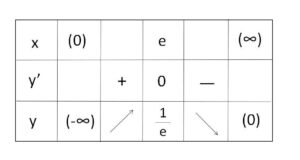
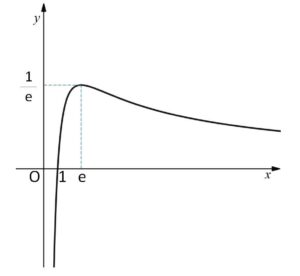
(3)
\(\displaystyle\frac{\log a}{a}=\displaystyle\frac{\log b}{b}\)
となり、どちらも同じ形になります。\(a,b\)は異なる正の数なので、この等式が成り立つ\(a,b\)が存在するためには、\(\displaystyle\frac{\log x}{x}=k\) が異なる2つ以上の正の解をもつ(グラフが2つ以上の交点をもつ)場合を考えればよいことになります。
グラフより交点は2つまでしかもたず、小さいほうの解のとりうる範囲が\(a\)の値の範囲になります。
\(a^b=b^a\) (\(a<b\)) ・・・① より
\(b\log a=a\log b\)
よって
\(\displaystyle\frac{\log a}{a}=\displaystyle\frac{\log b}{b}\)\((=k)\)
であり、\(y=\displaystyle\frac{\log x}{x}\) と \(y=k\) のグラフが2点以上で交わる場合を考えると、\(0<k<\displaystyle\frac{1}{e}\)
このとき、2交点のうち\(x\)座標が小さいほうの\(x\)座標が\(a\)となるから、①が成り立つ\(b\)が存在する\(a\)の範囲は
\(1<a<e\)
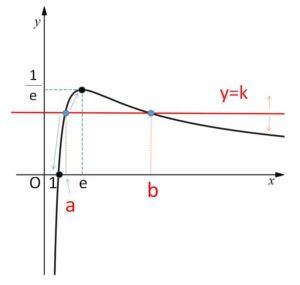
(4)
\(e≒2.7\) なので、\(s=2\) が決定します。\(t\)については、\(\displaystyle\frac{\log x}{x}=\displaystyle\frac{\log 2}{2}\) となるような\(x\)を、\(x=3,4,5,\cdots\) と代入していって探してもよいですし、もとの方程式 \(2^t=t^2\) から 適当に代入して成り立つ\(t\)を探してもよいです。(グラフより\(t\)は1つしかありません)
\(s^t=t^s\) (\(s<t\))
(3)と同様に考えると
\(\displaystyle\frac{\log s}{s}=\displaystyle\frac{\log t}{t}\)
\(1<s<e\)
\(s\)は正の整数だから、\(s=2\)
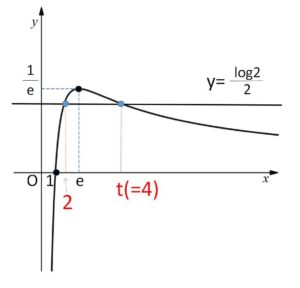
またグラフより、\(s=2\) に対応する\(t\)は1通りしかなく
\(\displaystyle\frac{\log 4}{4}=\displaystyle\frac{2\log 2}{4}=\displaystyle\frac{\log 2}{2}\)
となるから、\(t=4\)。
答 \(s=2\)、\(t=4\)
(例題2)
すべての正の実数\(x\)について、\(x^{\sqrt{a}}≦a^{\sqrt{x}}\) となる正の実数\(a\)を求めよ。
(解答)
\(x^{\sqrt{a}}≦a^{\sqrt{x}}\) (\(x>0\)、\(a>0\))
対数を取って
\(\sqrt{a}\log x≦\sqrt{x}\log a\)
よって
\(\displaystyle\frac{\log x}{\sqrt{x}}≦\displaystyle\frac{\log a}{\sqrt{a}}\)
が、任意の正の実数\(x\)で成り立つような\(a\)を求めればよい。
\(f(x)=\displaystyle\frac{\log x}{\sqrt{x}}\) (\(x>0\))
とおくと
\(f'(x)=\displaystyle\frac{\displaystyle\frac{1}{x}\cdot\sqrt{x}-\log x\cdot\displaystyle\frac{1}{2\sqrt{x}}}{x}\)
\(=\displaystyle\frac{2-\log x}{2x\sqrt{x}}\)
ゆえに増減表とグラフは次の通り。

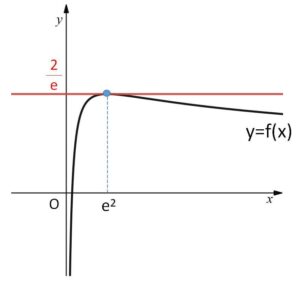
グラフより
\(f(x)≦\displaystyle\frac{\log a}{\sqrt{a}}\)
が任意の正の数\(x\)で成り立つためには
\(\displaystyle\frac{\log a}{\sqrt{a}}≧\displaystyle\frac{2}{e}\)・・・①
また、\((a,\displaystyle\frac{\log a}{\sqrt{a}})\) は \(y=f(x)\) 上の点であり、\(f(x)\)の最大値が\(\displaystyle\frac{2}{e}\)だから
\(\displaystyle\frac{\log a}{\sqrt{a}}≦\displaystyle\frac{2}{e}\)・・・②
①②より
\(\displaystyle\frac{\log a}{\sqrt{a}}=\displaystyle\frac{2}{e}\)
\(f(x)\)は\(x=e^2\)で最大値\(\displaystyle\frac{2}{e}\)をとるから
\(a=e^2\)
が同じ形であることに着目して、\(f(x)\)の最大値が\(\displaystyle\frac{2}{e}\) (\(x=e^2\) のとき)だから、この不等式が任意の正の数\(x\)で成り立つためには
\(\displaystyle\frac{\log a}{\sqrt{a}}=\displaystyle\frac{2}{e}\)
つまり、\(a=e^2\) と判断してもよいです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→n次方程式の解と微分 back→接線の本数