平面上の運動です。
・平面上の運動
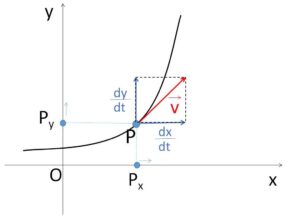
座標平面上を運動する点\(P(x,y)\)があり、座標\(x,y\)が時刻\(t\)の関数として
\(x=f(t)\)、\(y=g(t)\)・・・①
と表されているとします。
このとき、点\(P\)から\(x,y\)軸に下ろした垂線の足を\(P_x,P_y\)とすると(つまり影を考えると)、点\(P_x,P_y\)は軸上を直線運動します。
①より 点\(P_x\)の速度は\(\displaystyle\frac{dx}{dt}(f'(t))\)、点\(P_y\)の速度は\(\displaystyle\frac{dy}{dt}(g'(t))\) で表され、これらをそれぞれ点\(P\)の\(x,y\)軸方向の速度といいます。そしてこれらの速度から作られるベクトル
\(\vec{v}=(\displaystyle\frac{dx}{dt},\displaystyle\frac{dy}{dt})\)
を点\(P\)の速度(速度ベクトル)とします。つまり平面上の運動を扱うときは、\(x,y\)軸方向に分解して分析することになります。
なお、\(\vec{v}\) 方向の直線の傾きは \(\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}=\displaystyle\frac{dy}{dx}\) となるので、点\(P\)から\(\vec{v}\) 方向に直線をひくと、この直線は点\(P\)が描く曲線の接線になっています。
また平面上の速さ(速度の大きさ)は、上記ベクトルの大きさ\(|\vec{v}|\)とします。(全体としてのベクトルの大きさとする)
\(|\vec{v}|=\sqrt{(\displaystyle\frac{dx}{dt})^2+(\displaystyle\frac{dy}{dt})^2}\)
同様にして点\(P\)の\(x,y\)軸方向の加速度を\(\displaystyle\frac{d^2x}{dt^2}\)、\(\displaystyle\frac{d^2y}{dt^2}\)とし
点\(P\)の加速度(加速度ベクトル)\(\vec{α}\)を
\(\vec{α}=(\displaystyle\frac{d^2x}{dt^2},\displaystyle\frac{d^2y}{dt^2})\)
として、加速度の大きさを\(|\vec{α}|\)とします。
\(|\vec{α}|=\sqrt{(\displaystyle\frac{d^2x}{dt^2})^2+(\displaystyle\frac{d^2y}{dt^2})^2}\)
(例題)
座標平面上を運動する点\(P\)の時刻\(t\)における座標\((x,y)\)が
\(x=\sin t\)、\(y=\displaystyle\frac{1}{2}\cos2t\)
で表されているとする。このとき、点\(P\)は曲線 ( 1 ) 上を動く。また、点\(P\)の速度ベクトルは \(\vec{v}=\) ( 2 ) であり、加速度ベクトルは \(\vec{α}=\) ( 3 ) である。
速さ \(|\vec{v}|\) が\(0\)になるとき、点\(P\)は点\(Q\)( 4 ) あるいは 点\(R\)( 5 ) の位置にある(ただし、\(Q\)の\(x\)座標>\(R\)の\(x\)座標 とする)。\(0≦t≦30\) において、点\(P\)は定点\(Q\)を ( 6 ) 回通る。
\(|\vec{v}|\) の最大値は ( 7 ) であり、加速度の大きさ\(|\vec{α}|\) の最小値は ( 8 ) である。
(解答)
(1)
(\(t\)は簡単に消去できます)
\(y=\displaystyle\frac{1}{2}\cos2t=\displaystyle\frac{1}{2}(1-2\sin^2t)\) より
\(y=-x^2+\displaystyle\frac{1}{2}\)
(2)(3)
\(x=\sin t\)、\(y=\displaystyle\frac{1}{2}\cos2t\) より順次微分して
\(\vec{v}=(\cos t,-\sin 2t)\)
\(\vec{α}=(-\sin t,-2\cos2t)\)
(4)(5)
\(|\vec{v}|=\sqrt{\cos^2t+\sin^22t}\)
\(=\sqrt{\cos^2t+4\sin^2t\cos^2t}\)
\(=\sqrt{\cos^2t(1+4\sin^2t)}\)
\(1+4\sin^2t>0\) だから \(|\vec{v}|=0\) のとき
\(\cos t=0\)
よって、\(t=\displaystyle\frac{π}{2}+nπ\) (\(n\)は整数)
だから
\(x\)\(=\sin(\displaystyle\frac{π}{2}+nπ)\)\(=±1\)
\(y\)\(=\displaystyle\frac{1}{2}\cos2(\displaystyle\frac{π}{2}+nπ)=\displaystyle\frac{1}{2}\cos(π+2nπ)=\displaystyle\frac{1}{2}\cosπ\)\(=-\displaystyle\frac{1}{2}\)
\(Q\)の\(x\)座標のほうが大きいから
\(Q(1,-\displaystyle\frac{1}{2})\)、\(R(-1,-\displaystyle\frac{1}{2})\)
(6)
\(Q(1,-\displaystyle\frac{1}{2})\) を通るとき
\(x=\sin t\)、\(y=\displaystyle\frac{1}{2}\cos2t\) より
\(t=\displaystyle\frac{π}{2}+2nπ\) (\(n\)は整数)
だから、\(0≦t≦30\) を満たすのは \(n=0,1,2,3,4\)
(\(π≒3.14\) として、\(\displaystyle\frac{π}{2}≒1.57\)、\(\displaystyle\frac{π}{2}+8π≒26.69\))
よって\(Q\)を通る回数は\(5\)回。
(7)
(4)(5)より
\(|\vec{v}|\)
\(=\sqrt{\cos^2t(1+4\sin^2t)}\)
(三角関数の種類を統一すると)
\(=\sqrt{\cos^2t(5-4\cos^2t)}\)
\(=\sqrt{-4\cos^4t+5\cos^2t}\)
(複2次式(2次式の2次式)だから、平方完成した方が楽です)
\(=\sqrt{-4(\cos^2t-\displaystyle\frac{5}{8})^2+\displaystyle\frac{25}{16}}\)
よって \(\cos^2t=\displaystyle\frac{5}{8}\) のとき最大値 \(\sqrt{\displaystyle\frac{25}{16}}=\)\(\displaystyle\frac{5}{4}\) をとる。
(8)
\(\vec{α}=(-\sin t,-2\cos2t)\) より
\(|\vec{α}|=\sqrt{\sin^2t+4\cos^22t}\)
(同様に1種類の三角関数に統一すると)
\(=\sqrt{\sin^2t+4(1-2\sin^2t)^2}\)
\(=\sqrt{16\sin^4t-15\sin^2t+4}\)
\(=\sqrt{16(\sin^2t-\displaystyle\frac{15}{32})^2-\displaystyle\frac{15^2}{64}+4}\)
\(=\sqrt{16(\sin^2t-\displaystyle\frac{15}{32})^2+\displaystyle\frac{31}{64}}\)
よって、\(\sin^2t=\displaystyle\frac{15}{32}\) のとき、最小値 \(\displaystyle\frac{\sqrt{31}}{8}\) をとる。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→円運動と単振動 back→速度・加速度(直線上の運動)