グラフの上の点の速度・加速度

曲線上を運動する点の例題です。

(例題)
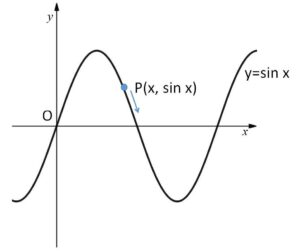
\(xy\)平面上の曲線 \(y=\sin x\) に沿って、左から右へ進む動点\(P\)がある。\(P\)の速さが一定値 \(v\) (\(v>0\)) であるとき、次の問いに答えよ。

(1)\(P\)が点\((x,\sin x)\) を通過する時刻での速度ベクトルを\(x\)と\(v\)を用いて表せ。
(2)\(P\)が点\((x,\sin x)\) を通過する時刻での加速度ベクトルを\(x\)と\(v\)を用いて表せ。
(3)加速度の大きさの最大値を\(v\)を用いて表せ。

時刻を\(t\)とすると、\(t\)秒後の点\(P\)の位置は1通りに決まるので、\(x,y\)は\(t\)の関数となります。しかしこの問題は\(x,y\)を\(t\)で表さずに解いていくところがポイントになります。
(3)が本題ですが、(1)(2)の誘導では合成関数の微分がポイントとなります。

グラフ上運動1

(解答)
(1)
点\(P(x,\sin x)\) における速度ベクトル\(\vec{v}\)は、\(t\)で微分すると
\(\vec{v}=(\displaystyle\frac{dx}{dt},\ \displaystyle\frac{d}{dx}(\sin x)\cdot\displaystyle\frac{dx}{dt})\)

\(=(\displaystyle\frac{dx}{dt},\ \cos x\cdot\displaystyle\frac{dx}{dt})\)・・・①

\(P\)の速さは\(v\)なので
\((\displaystyle\frac{dx}{dt})^2+\cos^2x(\displaystyle\frac{dx}{dt})^2=v^2\)

よって
\((\displaystyle\frac{dx}{dt})^2=\displaystyle\frac{v^2}{1+\cos^2x}\)

\(P\)は左から右へ進むので、\((\displaystyle\frac{dx}{dt})^2≧0\) より
\(\displaystyle\frac{dx}{dt}=\displaystyle\frac{v}{\sqrt{1+\cos^2x}}\)

よって①より
\(\vec{v}=(\displaystyle\frac{v}{\sqrt{1+\cos^2x}},\displaystyle\frac{v\cos x}{\sqrt{1+\cos^2x}})\)

速度ベクトルは\(t\)で表されていませんが、\(x\)のみの式になっているので、具体的に\(x\)の座標を代入することで、速度を求めることができます。例えば原点を通るときの速度は \(x=0\) を代入して \(\vec{v}=(\displaystyle\frac{v}{\sqrt{2}},\displaystyle\frac{v}{\sqrt{2}})\) です。

(2)
(1)の結果
\(\vec{v}=(\displaystyle\frac{v}{\sqrt{1+\cos^2x}},\displaystyle\frac{v\cos x}{\sqrt{1+\cos^2x}})\) より、加速度ベクトル\(\vec{α}\)は\(t\)で微分すると

\(x\)成分について
\(\displaystyle\frac{d}{dx}(\displaystyle\frac{v}{\sqrt{1+\cos^2x}})\cdot\displaystyle\frac{dx}{dt}\)

\(=-\displaystyle\frac{v}{2}\cdot(1+\cos^2x)^{-\frac{3}{2}}\cdot(-2\cos x\sin x)\cdot(\displaystyle\frac{v}{\sqrt{1+\cos^2x}})\)

\(=\displaystyle\frac{v^2\sin x\cos x}{(1+\cos^2x)^2}\)

\(y\)成分について
\(\displaystyle\frac{d}{dx}(\displaystyle\frac{v\cos x}{\sqrt{1+\cos^2x}})\cdot\displaystyle\frac{dx}{dt}\)

\(=v\cdot\displaystyle\frac{-\sin x\sqrt{1+\cos^2x}-\cos x(\displaystyle\frac{-2\cos x\sin x}{2\sqrt{1+\cos^2x}})}{1+\cos^2x}\cdot(\displaystyle\frac{v}{\sqrt{1+\cos^2x}})\)

\(=v^2\cdot\displaystyle\frac{-\sin x(1+\cos^2x)+\sin x\cos^2x}{(1+\cos^2x)^2}\)

\(=\displaystyle\frac{-v^2\sin x}{(1+\cos^2x)^2}\)

となるから
\(\vec{α}=(\displaystyle\frac{v^2\sin x\cos x}{(1+\cos^2x)^2},\displaystyle\frac{-v^2\sin x}{(1+\cos^2x)^2})\)

(3)
(2)より
\(|\vec{α}|=\sqrt{\displaystyle\frac{v^4\sin^2x\cos^2x}{(1+\cos^2x)^4}+\displaystyle\frac{v^4\sin^2x}{(1+\cos^2x)^4}}\)

\(=v^2\sqrt{\displaystyle\frac{\sin^2x(1+\cos^2x)}{(1+\cos^2x)^4}}\)

\(=v^2\sqrt{\displaystyle\frac{\sin^2x}{(1+\cos^2x)^3}}\)

\(\sin\) か \(\cos\) に統一して、2乗の部分を置きかえて微分してもよいですが、\(\sin ^2x\) の最大値は\(1\)、\(1+\cos^2x\) の最小値は\(1\) であり、このときが考えうる一番大きい値で、実現すれば最大値になります。(\(x=\displaystyle\frac{π}{2}+nπ\) で実現する)

よって
\(|\vec{α}|≦v^2\sqrt{\displaystyle\frac{(±1)^2}{(1+0)^3}}\)

\(|\vec{α}|≦v^2\)

等号は \(\sin x=±1\) のとき (このとき \(\cos x=0\)) 成立するから
加速度の大きさの最大値は \(v^2\)

自分がこの曲線上を一定の速さで走っている時を考えると、一番きつい(力がいる)ところは \(y=±1\) の折り返す部分でしょう。ニュートンの運動方程式によると力と加速度は比例関係にあるので、加速度が \(y=±1\) のときに一番大きくなるのも感覚的にうなずけます。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→変化率(体積・表面積の変化など)　back→円運動と単振動